题目内容
已知θ为第二象限角,且sinθ+cosθ=
,那么tanθ=( )
| 1 |
| 5 |
A.-
| B.-
| C.-
| D.-
|
因为sinx+cosx=
,而sin2x+cos2x=1
即(sinx+cosx)2-2sinxcosx=1,所以
-2sinxcosx=1
所以2sinxcosx=-
又因为sin2x+cos2x=(sinx-cosx)2+2sinxcosx=1
所以(sinx-cosx)2-
=1,所以(sinx-cosx)2=
又因为0<x<180°,所以sinx>0,而2sinxcosx=-
<0,所以cosx<0
所以sinx-cosx>0,所以sinx-cosx=
和sinx+cosx=
相加得:sinx=
,所以cosx=-
所以tanx=-
故选B
| 1 |
| 5 |
即(sinx+cosx)2-2sinxcosx=1,所以
| 1 |
| 25 |
所以2sinxcosx=-
| 24 |
| 25 |
又因为sin2x+cos2x=(sinx-cosx)2+2sinxcosx=1
所以(sinx-cosx)2-
| 24 |
| 25 |
| 49 |
| 25 |
又因为0<x<180°,所以sinx>0,而2sinxcosx=-
| 24 |
| 25 |
所以sinx-cosx>0,所以sinx-cosx=
| 7 |
| 5 |
和sinx+cosx=
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
所以tanx=-
| 4 |
| 3 |
故选B

练习册系列答案
相关题目
 ,则2a是( )
,则2a是( ) ,
, 为第二象限角,求
为第二象限角,求 ;
; ,求
,求 的值。
的值。 ,
, 为第二象限角,求
为第二象限角,求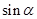 和
和 及
及 的值.
的值.