题目内容
已知函数f（x）=
有三个不同的零点，则实数a的取值范围是________．
a＞4
分析：由题意可得函数f（x）的图象与x轴有三个不同的交点，结合图象求出实数a的取值范围．
解答：
解：由题意可得函数f（x）的图象与x轴有三个不同的交点，如图所示：
等价于当x≥0时，方程2x-a=0有一个根，且x＜0时，方程x2+ax+a=0有两个根，
即
?a＞4．
故实数a的取值范围是a＞4．
故答案为：a＞4．
点评：本题主要考查函数的零点与方程的根的关系，体现了化归与转化、数形结合的数学思想，属于中档题．
分析：由题意可得函数f（x）的图象与x轴有三个不同的交点，结合图象求出实数a的取值范围．
解答：
解：由题意可得函数f（x）的图象与x轴有三个不同的交点，如图所示：等价于当x≥0时，方程2x-a=0有一个根，且x＜0时，方程x2+ax+a=0有两个根，
即
?a＞4．故实数a的取值范围是a＞4．
故答案为：a＞4．
点评：本题主要考查函数的零点与方程的根的关系，体现了化归与转化、数形结合的数学思想，属于中档题．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
已知函数f（x）=loga（2+x）-loga（2-x）（a＞0，a≠1），设f（x）的反函数为f-1（x）．若关于x的不等式f-1（x）＜m（m∈R）有解，则m的取值范围是（ ）
| A、m＞-2 | B、m＞2 | C、-2＜m＜2 | D、随a的变化而变化 |
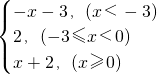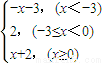，有下面四个结论：
，有下面四个结论：
，有下面四个结论：