题目内容
已知函数
．
（1）求f（x）的定义域；
（2）用单调性定义证明函数
在（0，+∞）上单调递增．
．（1）求f（x）的定义域；
（2）用单调性定义证明函数
在（0，+∞）上单调递增．解：（1）f（x）的定义域为{x|x≠0}
（2）在（0，+∞）内任取x1，x2，
令x1＜x2，
=
∵x1＜x2，
∴x1﹣x2＞0
∵x1，x2∈（0，+∞），
∴x1x2＞0
∴
∴f（x1）﹣f（x2）＜0即f（x1）＜f（x2）
∴
在（0，+∞）上单调递增．
（2）在（0，+∞）内任取x1，x2，
令x1＜x2，
=
∵x1＜x2，
∴x1﹣x2＞0
∵x1，x2∈（0，+∞），
∴x1x2＞0
∴
∴f（x1）﹣f（x2）＜0即f（x1）＜f（x2）
∴
在（0，+∞）上单调递增．
练习册系列答案
相关题目
．
．
的图象在x轴上方？
．
为f（x）的一个零点，求sin2x的值．
．
．
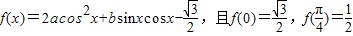，求f（x）的最大值和最小值．