题目内容
已知函数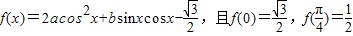 .
.(1)求f(x)的最小正周期;
(2)求f(x)的单调递减区间;
(3)函数f(x)的图象经过怎样的平移才能使其对应的函数成为奇函数?
【答案】分析:(1)先由f(0)= 求得a,由
求得a,由 求得b,进而求得函数f(x)的解析式,利用二倍角公式和两角和公式化简整理,进而根据T=
求得b,进而求得函数f(x)的解析式,利用二倍角公式和两角和公式化简整理,进而根据T= 求得函数的最小正周期.
求得函数的最小正周期.
(2)根据正弦函数的单调性可求得当函数单调减时2x+ 的范围,进而求得x的范围,即函数的单调性减区间.
的范围,进而求得x的范围,即函数的单调性减区间.
(3)根据函数的解析式可知奇函数的图象左移 即得到f(x)的图象,进而可推断出函数f(x)的图象右移
即得到f(x)的图象,进而可推断出函数f(x)的图象右移 后对应的函数成为奇函数.
后对应的函数成为奇函数.
解答:解:(1)由 ,∴
,∴ ,
,
由 ,∴b=1,
,∴b=1,
∴ .
.
∴函数f(x)的最小正周期T= .
.
(2)由 ,
,
∴f(x)的单调递减区间是 (k∈Z).
(k∈Z).
(3)∵ ,
,
∴奇函数的图象左移 即得到f(x)的图象,
即得到f(x)的图象,
故函数f(x)的图象右移 后对应的函数成为奇函数.
后对应的函数成为奇函数.
点评:本题主要考查了三角函数的周期及其求法,三角函数的单调性,函数图象的平移,考查了对基础知识的综合把握.
 求得a,由
求得a,由 求得b,进而求得函数f(x)的解析式,利用二倍角公式和两角和公式化简整理,进而根据T=
求得b,进而求得函数f(x)的解析式,利用二倍角公式和两角和公式化简整理,进而根据T= 求得函数的最小正周期.
求得函数的最小正周期.(2)根据正弦函数的单调性可求得当函数单调减时2x+
 的范围,进而求得x的范围,即函数的单调性减区间.
的范围,进而求得x的范围,即函数的单调性减区间.(3)根据函数的解析式可知奇函数的图象左移
 即得到f(x)的图象,进而可推断出函数f(x)的图象右移
即得到f(x)的图象,进而可推断出函数f(x)的图象右移 后对应的函数成为奇函数.
后对应的函数成为奇函数.解答:解:(1)由
 ,∴
,∴ ,
,由
 ,∴b=1,
,∴b=1,∴
 .
.∴函数f(x)的最小正周期T=
 .
.(2)由
 ,
,∴f(x)的单调递减区间是
 (k∈Z).
(k∈Z).(3)∵
 ,
,∴奇函数的图象左移
 即得到f(x)的图象,
即得到f(x)的图象,故函数f(x)的图象右移
 后对应的函数成为奇函数.
后对应的函数成为奇函数.点评:本题主要考查了三角函数的周期及其求法,三角函数的单调性,函数图象的平移,考查了对基础知识的综合把握.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.