Question

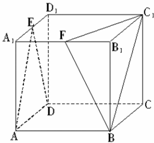如图，在棱长为1的正方体AC₁中，E、F分别为A₁D₁和A₁B₁的中点．
（1）求异面直线AE和BF所成的角的余弦值；
（2）求平面BDD₁与平面BFC₁所成的锐二面角的余弦值．

Answer 1

分析：（1）以D为原点，DA为x轴建立坐标系，写出要用的点的坐标，写出两条直线的方向向量，根据两个向量的夹角点的两条异面直线的夹角．
（2）要求两个平面的夹角，先求出两个向量的法向量，根据两个向量的法向量所成的角的余弦，点的两个平面所成的角的余弦值．

解答：解：（1）建立坐标系，以D为原点，DA为x轴建立坐标系
A（1，0，0），E(

1

2

，0，1)，B（1，1，0），F(1，

1

2

，1)

AE

=(-

1

2

，0，1)，

BF

=(0，-

1

2

，1)
cos(

AE

，

BF

)=

1

5 4 5 4

=

4

5

异面直线AE和BF所成的角的余弦值是

4

5

；
（2）平面BDD₁的一个法向量为

MA

=(

1

2

，-

1

2

，0)
设平面BFC₁的法向量为

n

=(x，y，z)

n • BF =- 1 2 y+z=0 n • BC =(x，y，z)•(-1，0，1)=-x+z=0

∴

x=z y=2z

取z=1得平面BFC₁的一个法向量

n

=(1，2，1)
cos＜

MA

，

n

＞=

MA • n

| MA || n |

=

1 2 -1

2 2 6

=-

3

6

，
∴所求的余弦值为

3

6

点评：本题考查利用空间向量解决立体几何中的夹角问题，本题解题的关键是建立坐标系，把理论的推导转化成数字的运算．