题目内容
△ABC中, =(cosA,sinA),
=(cosA,sinA), =(cosB,-sinB),若
=(cosB,-sinB),若 •
• =
= ,则角C为
,则角C为
- A.

- B.

- C.

- D.

B
分析:利用数量积和三角形的内角和定理、诱导公式即可化简,再利用三角形内特殊角的三角函数值即可得出.
解答:∵ =(cosA,sinA),
=(cosA,sinA), =(cosB,-sinB),
=(cosB,-sinB),
∴ =cosAcosB-sinAsinB=cos(A+B)=cos(π-C)=-cosC,
=cosAcosB-sinAsinB=cos(A+B)=cos(π-C)=-cosC,
∴ ,得cosC=-
,得cosC=- .
.
∵0<C<π.
∴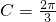 .
.
故选B.
点评:熟练掌握数量积和三角形的内角和定理、诱导公式、三角形内角的特殊角的三角函数值是解题的关键.
分析:利用数量积和三角形的内角和定理、诱导公式即可化简,再利用三角形内特殊角的三角函数值即可得出.
解答:∵
 =(cosA,sinA),
=(cosA,sinA), =(cosB,-sinB),
=(cosB,-sinB),∴
 =cosAcosB-sinAsinB=cos(A+B)=cos(π-C)=-cosC,
=cosAcosB-sinAsinB=cos(A+B)=cos(π-C)=-cosC,∴
 ,得cosC=-
,得cosC=- .
.∵0<C<π.
∴
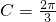 .
.故选B.
点评:熟练掌握数量积和三角形的内角和定理、诱导公式、三角形内角的特殊角的三角函数值是解题的关键.

练习册系列答案
相关题目
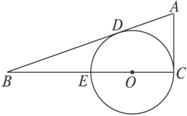
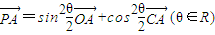 ,则
,则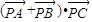 的最小值是 .
的最小值是 .