题目内容
4. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AD∥BC,且AB=2BC=4,PA=AD=3,∠ABC=60°,E是BC的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AD∥BC,且AB=2BC=4,PA=AD=3,∠ABC=60°,E是BC的中点.(1)求证:AD⊥平面PAC;
(2)试在线段PD上确定一点G,使CG∥平面PAE,并求此时AD与平面AGC所成角的正弦值.
分析 (1)由勾股定理得AD⊥AC,由线面垂直得AD⊥AP,由此能证明AD⊥平面PAC.
(2)以A为原点,AC为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法求出G(-2$\sqrt{3}$,1,2),由此能求出AD与平面AGC所成角的正弦值.
解答 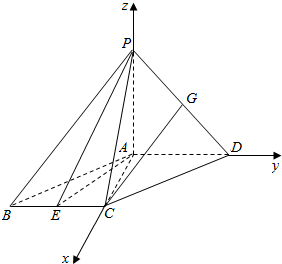 (1)证明:∵AB=2BC=4,∠ABC=60°,E是BC的中点,
(1)证明:∵AB=2BC=4,∠ABC=60°,E是BC的中点,
∴AC=$\sqrt{16+4-2×4×2×60°}$=2$\sqrt{3}$,
∴AB2=BC2+AC2,
∵底面ABCD为梯形,AD∥BC,∠ABC=60°,
∴AD⊥AC,
∵在四棱锥P-ABCD中,PA⊥平面ABCD,AD?平面ABCD,
∴AD⊥AP,
∵AP∩AC=A,∴AD⊥平面PAC.
(2)解:以A为原点,AC为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
由已知得C(2$\sqrt{3}$,0,0),A(0,0,0),P(0,0,3),D(0,3,0),E(2$\sqrt{3}$,-1,0),
设$\overrightarrow{PG}$=t$\overrightarrow{PD}$,0≤t≤1,设G(a,b,c),
则(a,b,c-3)=t(0,3,-3),∴G(0,3t,3-3t),∴$\overrightarrow{CG}$=(-2$\sqrt{3}$,3t,3-3t),
$\overrightarrow{AE}$=(2$\sqrt{3}$,-1,0),$\overrightarrow{AP}$=(0,0,3),
设平面APE的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AE}=2\sqrt{3}x-y=0}\\{\overrightarrow{n}•\overrightarrow{AP}=3z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,2$\sqrt{3}$,0),
∵CG∥平面PAE,∴$\overrightarrow{CG}•\overrightarrow{n}$=-2$\sqrt{3}$+6$\sqrt{3}t$=0,解得t=$\frac{1}{3}$,∴G(-2$\sqrt{3}$,1,2),
$\overrightarrow{AD}$=(0,3,0),$\overrightarrow{AC}$=(2$\sqrt{3}$,0,0),$\overrightarrow{AG}$=(-2$\sqrt{3}$,1,2),
设平面ACG的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AC}=2\sqrt{3}a=0}\\{\overrightarrow{m}•\overrightarrow{AG}=-2\sqrt{3}a+b+2c=0}\end{array}\right.$,取b=2,得$\overrightarrow{m}$=(0,2,-1),
设AD与平面AGC所成角为θ,
则sinθ=|cos<$\overrightarrow{m},\overrightarrow{n}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$|=$\frac{4\sqrt{3}}{\sqrt{13}•\sqrt{5}}$=$\frac{4\sqrt{195}}{65}$.
∴AD与平面AGC所成角的正弦值为$\frac{4\sqrt{195}}{65}$.
点评 本题考查线面垂直的证明、考查线面所成角的正弦值的求法,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

 小学课时特训系列答案
小学课时特训系列答案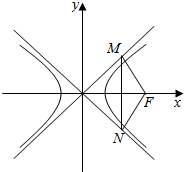 如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )| A. | (1,$\sqrt{2}$) | B. | (1,2) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
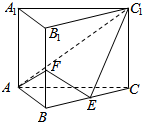 已知在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,E,F分别是BC,BB1的中点.
已知在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,E,F分别是BC,BB1的中点. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=AB,点M在棱PD上,PB∥平面ACM.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=AB,点M在棱PD上,PB∥平面ACM.