题目内容
9.已知函数f(x)是R上的奇函数,且对任意实数x满足f(x)+f(x+$\frac{3}{2}$)=0,若f(1)>1,f(2)=a,则实数a的取值范围是a<-1.分析 首先,根据f(x+$\frac{3}{2}$)=-f(x),得到f(x)是周期为3的函数,然后,得到f(1)=-a,再结合f(1)>1,得到答案.
解答 解:∵f(x)+f(x+$\frac{3}{2}$)=0,
∴f(x+$\frac{3}{2}$)=-f(x),
∴f(x+3)=f(x),
∴f(x)是周期为3的函数,
∵f(2)=f(3-1)=f(-1)=-f(1)=a
∴f(1)=-a
又∵f(1)>1,
∴-a>1,
∴a<-1
故答案为a<-1.
点评 本题综合考查了奇函数的性质、周期函数、对数函数的单调性等知识,属于中档题.注意分类讨论思想在解题中的灵活运用.

练习册系列答案
相关题目
19.全集U={1,2,3,4,5},集合A={1,2},集合B={1,3,5},则图中阴影部分所表示的集合是( )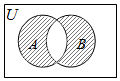

| A. | {1} | B. | {1,2,3,5} | C. | { 2,3,5} | D. | {4} |
 如图,已知E、F两点分别是正方形ABCD边AD、AB的中点,EF交AC于点M,GC垂直于ABCD所在平面.
如图,已知E、F两点分别是正方形ABCD边AD、AB的中点,EF交AC于点M,GC垂直于ABCD所在平面.