题目内容
已知常数a>0且a≠1,变数x、y满足 3logxa+logax-logxy=3(1)若x=at(t≠0),试以a、t表示y.
(2)若t∈{t|t2-4t+3≤0}时,y有最小值8,求a和x的值.
【答案】分析:(1)由题意利用换底公式可得 logay=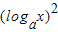 -3logax+3,再由x=at(t≠0),可得 logax=t,由此可用a、t表示y.
-3logax+3,再由x=at(t≠0),可得 logax=t,由此可用a、t表示y.
(2)由t2-4t+3≤0可得 1≤t≤3.分0<a<1和a>1两种情况,并根据y有最小值8,求得a的值,由此求得对应的x的值.
解答:解:(1)∵3logxa+logax-logxy=3,由换底公式可得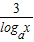 +logax-
+logax-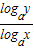 =3,
=3,
解得 logay=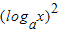 -3logax+3.
-3logax+3.
若x=at(t≠0),则 logax=t,
∴logay=t2-3t+3,∴y=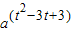 .
.
(2)由t2-4t+3≤0可得 1≤t≤3.
当0<a<1时,由于y有最小值8,故函数u=t2-3t+3=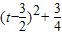 必有最大值,故当 t=3时,函数u取得最大值为3,即 a3=8,a=2,这与0<a<1矛盾.
必有最大值,故当 t=3时,函数u取得最大值为3,即 a3=8,a=2,这与0<a<1矛盾.
当a>1时,由于y有最小值8,故函数u=t2-3t+3=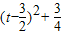 必有最小值,故当 t=
必有最小值,故当 t= 时,函数u取得最小值为
时,函数u取得最小值为 ,即
,即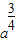 =8,a=16,此时x=64.
=8,a=16,此时x=64.
点评:本题主要考查对数函数的图象和性质,二次函数的性质应用,属于中档题.
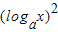 -3logax+3,再由x=at(t≠0),可得 logax=t,由此可用a、t表示y.
-3logax+3,再由x=at(t≠0),可得 logax=t,由此可用a、t表示y.(2)由t2-4t+3≤0可得 1≤t≤3.分0<a<1和a>1两种情况,并根据y有最小值8,求得a的值,由此求得对应的x的值.
解答:解:(1)∵3logxa+logax-logxy=3,由换底公式可得
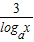 +logax-
+logax-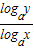 =3,
=3,解得 logay=
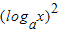 -3logax+3.
-3logax+3.若x=at(t≠0),则 logax=t,
∴logay=t2-3t+3,∴y=
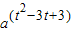 .
.(2)由t2-4t+3≤0可得 1≤t≤3.
当0<a<1时,由于y有最小值8,故函数u=t2-3t+3=
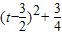 必有最大值,故当 t=3时,函数u取得最大值为3,即 a3=8,a=2,这与0<a<1矛盾.
必有最大值,故当 t=3时,函数u取得最大值为3,即 a3=8,a=2,这与0<a<1矛盾.当a>1时,由于y有最小值8,故函数u=t2-3t+3=
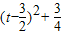 必有最小值,故当 t=
必有最小值,故当 t= 时,函数u取得最小值为
时,函数u取得最小值为 ,即
,即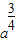 =8,a=16,此时x=64.
=8,a=16,此时x=64.点评:本题主要考查对数函数的图象和性质,二次函数的性质应用,属于中档题.

练习册系列答案
相关题目