题目内容
设区间[0,1]是方程f(x)=0的有解区间,画出用二分法求方程f(x)=0在区间[0,1]上的一个近似解的流程图,要求精确度为ε.
答案:
解析:
解析:
|
设置两个循环变量a,b,其初始值分别为0,1,终止条件为f( S1 由f(a)·f(b)<0,确定有解区间[a,b]; S2 取[a,b]的中点 S3 判断函数值f( ①如果为0,则x= ②如果不为0,则有两种情形. 若f(a)·f( S4 判断新的有解区间的长度是否小于ε. ①若大于ε,则在新的有解区间的基础上重复上述步骤;②若不大于ε,则取新的有解区间的中点为方程的近似解. 算法流程图如图所示.
|

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
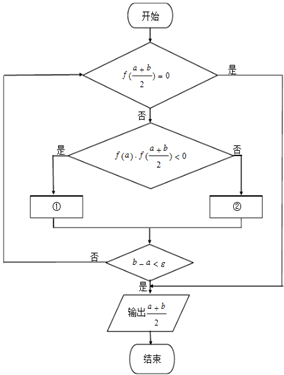 设区间[0,1]是方程f(x)=0的有解区间,用二分法求出方程f(x)=0在区间[0,1]上的一个近似解的流程图如图,设a,b∈[0,1],现要求精确度为ε,图中序号①,②处应填入的内容为( )
设区间[0,1]是方程f(x)=0的有解区间,用二分法求出方程f(x)=0在区间[0,1]上的一个近似解的流程图如图,设a,b∈[0,1],现要求精确度为ε,图中序号①,②处应填入的内容为( )A、a=
| ||||
B、b=
| ||||
C、a=
| ||||
D、b=
|
