Question

设函数f(x)=-ax,其中a＞0.若函数f(x)在［0,+∞)上是单调函数,求a的取值范围.

Answer 1

解:设取x₁,x₂∈［0,+∞),且x₁＜x₂,

f(x₁)-f(x₂)=-a(x₁-x₂)

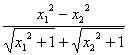=-a(x₁-x₂)=(x₁-x₂)(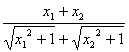-a).

(1)当a≥1时,由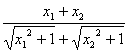＜1,易知f(x₁)＞f(x₂),所以,当a≥1时,函数f(x)在区间［0,+∞)上是单调递减函数.

(2)当0＜a＜1时,在区间［0,+∞)上存在两点x₁=0,x₂=,满足f(x₁)=f(x₂)=1,从而f(x)在［0,+∞)不是单调函数.

∴所求a的取值范围是a∈［1,+∞).