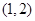题目内容
若不等式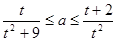 在
在 上恒成立,则
上恒成立,则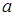 的取值范围是( )
的取值范围是( )
A.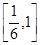 | B.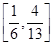 | C.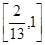 | D.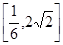 |
C
解析试题分析:因为不等式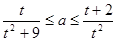 在
在 上恒成立,所以
上恒成立,所以 且
且 ,因为
,因为 ,所以
,所以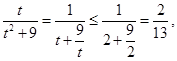
 ,所以
,所以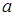 的取值范围是
的取值范围是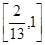 .
.
考点:本小题主要考查利用基本不等式、对数函数和二次函数求函数的最值,考查学生的转化能力和运算求解能力.
点评:恒成立问题一般转化成最值问题解决,而此小题求最值时,一定要注意变量的范围,当用基本不等式取不到等号时,要转化成对号函数求解.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
设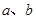 是互不相等的正数,则下列不等式中不恒成立的是( )
是互不相等的正数,则下列不等式中不恒成立的是( )
A.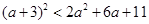 | B.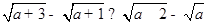 |
C.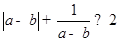 | D.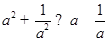 |
若不等式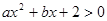 的解为
的解为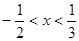 ,则
,则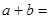 ( )
( )
| A.14 | B.-14 | C.-2 | D.12 |
若不等式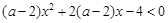 对一切
对一切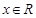 恒成立,则实数
恒成立,则实数 取值的集合( )
取值的集合( )
A.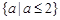 | B.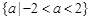 |
C.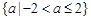 | D.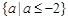 |
不等式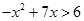 的解集是
的解集是
A.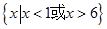 | B.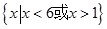 |
C.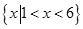 | D.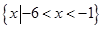 |
不等式 的解集为 ( )
的解集为 ( )
A. | B. |
C.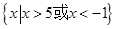 | D.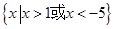 |
已知函数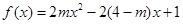 ,
,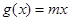 ,若对于任一实数
,若对于任一实数 ,
, 与
与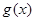 的值至少有一个为正数,则实数
的值至少有一个为正数,则实数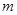 的取值范围是( )
的取值范围是( )
| A.(0,2) | B.(0,8) | C.(2,8) | D.(-∞,0) |
不等式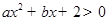 的解集是
的解集是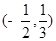 ,则
,则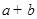 的值是( )
的值是( )
A.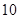 | B.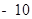 | C.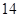 | D.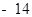 |
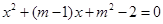 的两个实根一个小于0,另一个大于1,那么实数m的取值范围是( )
的两个实根一个小于0,另一个大于1,那么实数m的取值范围是( )