题目内容
已知函数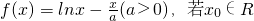
，使得?x1∈[1，2]，都有f（x1）＜f（x0），则实数a的取值范围是
- A.（0，1）
- B.（1，2）
- C.（2，+∞）
- D.（0，1）∪（2，+∞）
D
分析：求导函数，确定函数的单调性，进而可得函数的最大值，从而问题转化为最大值不在区间[1，2]，故可求实数a的取值范围．
解答：求导函数，
当x∈（0，a）时，f′（x）＞0，f（x）单调递增，当x∈（a，+∞）时，f′（x）＜0，f（x）单调递减，
故f（x）max=f（a）．
?x0∈R，使得?x1∈[1，2]，都有f（x1）＜f（x0），则最大值不在区间[1，2]，
∴a∉[1，2]，所以实数a的取值范围是（0，1）∪（2，+∞）
故选D．
点评：本题考查导数知识的运用，考查恒成立问题，考查函数的最值，属于中档题．
分析：求导函数，确定函数的单调性，进而可得函数的最大值，从而问题转化为最大值不在区间[1，2]，故可求实数a的取值范围．
解答：求导函数，
当x∈（0，a）时，f′（x）＞0，f（x）单调递增，当x∈（a，+∞）时，f′（x）＜0，f（x）单调递减，
故f（x）max=f（a）．
?x0∈R，使得?x1∈[1，2]，都有f（x1）＜f（x0），则最大值不在区间[1，2]，
∴a∉[1，2]，所以实数a的取值范围是（0，1）∪（2，+∞）
故选D．
点评：本题考查导数知识的运用，考查恒成立问题，考查函数的最值，属于中档题．
练习册系列答案
相关题目
已知函数f(x)=
(x∈R)时，则下列结论不正确的是（ ）
| x |
| 1+|x| |
| A、?x∈R，等式f（-x）+f（x）=0恒成立 |
| B、?m∈（0，1），使得方程|f（x）|=m有两个不等实数根 |
| C、?x1，x2∈R，若x1≠x2，则一定有f（x1）≠f（x2） |
| D、?k∈（1，+∞），使得函数g（x）=f（x）-kx在R上有三个零点 |
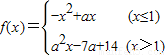，若?x1，x2∈R，且x1≠x2，使得f（x1）=f（x2），则实数a的取值范围是 ．