题目内容
已知圆x2+y2=1,点A(1,0),△ABC内接于该圆,且∠BAC=60°,当B、C在圆上运动时,求BC的中点的轨迹方程.
思路分析:本题是比较典型的使用曲线的参数方程来解决相关问题的题目,涉及到多个点的坐标.
解:如图2-1-1所示,M为BC的中点,
由∠BAC=60°,得∠BOC=2×60°=120°(弦所对的圆心角等于它所对的圆周角的2倍).
在△BOC中,OB=OC=1,所以OM=![]() .所以点M的轨迹方程为x2+y2=
.所以点M的轨迹方程为x2+y2=![]() .
.
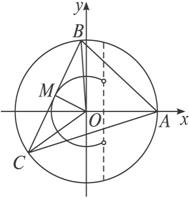
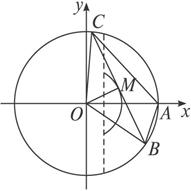
图2-1-1 图2-1-2
又因为x≥![]() 时,如图2-1-2.
时,如图2-1-2.
虽然∠BOC=120°,但∠BAC=![]() (360°-120°)=120°≠60°,
(360°-120°)=120°≠60°,
所以点M的轨迹方程为x2+y2=![]() (x<
(x<![]() ),如图2-1-2.
),如图2-1-2.
误区警示 本题主要容易忽视隐含的范围x<![]() ,忽视了这个范围则本题的解答就不严谨,并且很多资料上的答案也都没有这个范围,像这样的求轨迹的问题一定要注意这一点.
,忽视了这个范围则本题的解答就不严谨,并且很多资料上的答案也都没有这个范围,像这样的求轨迹的问题一定要注意这一点.

练习册系列答案
相关题目
已知圆x2+y2=1,点A(1,0),△ABC内接于圆,且∠BAC=60°,当B、C在圆上运动时,BC中点的轨迹方程是( )
A、x2+y2=
| ||||
B、x2+y2=
| ||||
C、x2+y2=
| ||||
D、x2+y2=
|
已知圆x2+y2=1与x轴的两个交点为A、B,若圆内的动点P使|PA|、|PO|、|PB|成等比数列,则
•
的取值范围为( )
| PA |
| PB |
A、(0,
| ||
B、[-
| ||
C、(-
| ||
| D、[-1,0) |
已知圆x2+y2=1和直线y=2x+b相交于A,B两点,且OA,OB是x轴正方向沿逆时针分别旋转α,β角而得,则cos(α+β)的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|