题目内容
已知函数 .
.
(1)用a表示f(2),f(3),并化简;
(2)比较 与
与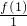 ,
, 与
与 的大小,并由此归纳出一个更一般的结论.(不要求写出证明过程).
的大小,并由此归纳出一个更一般的结论.(不要求写出证明过程).
解:(1)直接计算知:
f(2)=a+a-1,f(3)=a2+a-2+1,
(2) ,
, ,
, ,
,
根据基本不等式 ,
, ,
,
所以 .
.
归纳:?x>0, .
.
记 ,x>0,
,x>0,
 ,
,
设 ,
,
则h(0)=0且 ,
,
讨论知 ,
,
从而h(x)>h(0)=0,g′(x)>0,g(x)在R+上单调增加,
所以?x>0, .
.
分析:(1)直接计算f(2),f(3),即可;
(2)利用基本不等式和做差比较法比较大小,归纳结论,构造函数进行证明.
点评:本题考查比较大小、归纳推理、函数单调性的证明及应用,综合性强,难度较大.
f(2)=a+a-1,f(3)=a2+a-2+1,
(2)
 ,
, ,
, ,
,根据基本不等式
 ,
, ,
,所以
 .
.归纳:?x>0,
 .
.记
 ,x>0,
,x>0,
 ,
,设
 ,
,则h(0)=0且
 ,
,讨论知
 ,
,从而h(x)>h(0)=0,g′(x)>0,g(x)在R+上单调增加,
所以?x>0,
 .
.分析:(1)直接计算f(2),f(3),即可;
(2)利用基本不等式和做差比较法比较大小,归纳结论,构造函数进行证明.
点评:本题考查比较大小、归纳推理、函数单调性的证明及应用,综合性强,难度较大.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 .
. 与
与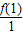 ,
,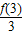 与
与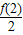 的大小,并由此归纳出一个更一般的结论.(不要求写出证明过程).
的大小,并由此归纳出一个更一般的结论.(不要求写出证明过程).