题目内容
已知![]() 图像上一点
图像上一点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的单调增区间;
的单调增区间;
(Ⅱ)令![]() ,如果
,如果![]() 图像与
图像与![]() 轴交于
轴交于![]() 两点,
两点,
![]() 的中点为
的中点为![]() ,问
,问![]() 在
在![]() 处是否取得极值.
处是否取得极值.
解:![]() ……1分
……1分
![]()
![]() 且
且![]()
解得:![]() ……1分
……1分
由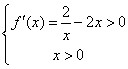 解得
解得![]()
![]() 的单调增区间是
的单调增区间是![]() ……2分
……2分
![]() ……1分
……1分
假设结论![]() 在
在![]() 处取极值,则
处取极值,则![]() 成立,则有
成立,则有
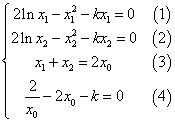
![]() 得
得![]()
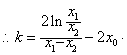
由![]() 得
得![]()
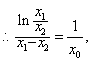
即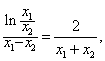
即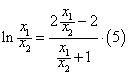
令![]()
![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
![]()
![]() ,
,![]() 式不成立,与假设矛盾,……6分
式不成立,与假设矛盾,……6分
故![]() 在
在![]() 处不是极值点。……1分
处不是极值点。……1分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 上任一点
上任一点 处的切线斜率
处的切线斜率 ,则该函数的单调递减区间为
,则该函数的单调递减区间为
A. | B. | C. | D. |
 上任一点
上任一点 处的切线斜率
处的切线斜率 ,则该函数的单调减区间为
,则该函数的单调减区间为  B.
B. C.
C. D.
D.