题目内容
若椭圆
与双曲线
的焦点相同，则椭圆的离心率e= ．
【答案】分析：据双曲线的方程判断出其焦点在x轴上，利用双曲线三参数的关系求出焦点坐标，再利用椭圆中三个参数的关系求出其离心率．
解答：解：双曲线
的焦点在x轴上
焦点坐标为（
，0）
∵
与双曲线
的焦点相同
∴4-a2=a+2
解得a=1
∴椭圆的离心率e=
故答案为：
．
点评：解决圆锥曲线的方程问题，要注意椭圆与双曲线它们的三个参数的关系的区别，椭圆中有b2+c2=a2；双曲线中b2+a2=c2
解答：解：双曲线
的焦点在x轴上焦点坐标为（
，0）∵
与双曲线的焦点相同∴4-a2=a+2
解得a=1
∴椭圆的离心率e=
故答案为：
．点评：解决圆锥曲线的方程问题，要注意椭圆与双曲线它们的三个参数的关系的区别，椭圆中有b2+c2=a2；双曲线中b2+a2=c2
练习册系列答案
相关题目
和双曲线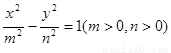
有相同的焦点F1、F2，以线段F1F2为边作正△F1F2M，若椭圆与双曲线的一个交点P恰好是MF1的中点，设椭圆和双曲线的离心率分别为
等于
与双曲线
的焦点相同，则椭圆的离心率e=________．
与双曲线
的焦点相同，则椭圆的离心率e= ．