题目内容
函数f(x)=
+
的定义域为
| x-2 |
| 1 |
| x-3 |
{x|x≥2且x≠3}
{x|x≥2且x≠3}
．分析：由函数解析式可得 x≥2 且x≠3，由此求得函数的定义域．
解答：解：由函数f(x)=
+
可得 x≥2 且x≠3，故函数f(x)=
+
的定义域为 {x|x≥2且x≠3}，
故答案为 {x|x≥2且x≠3}．
| x-2 |
| 1 |
| x-3 |
| x-2 |
| 1 |
| x-3 |
故答案为 {x|x≥2且x≠3}．
点评：本题主要考查求函数的定义域得方法，属于基础题．
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
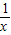是奇函数”的证明不是综合法的是（ ）
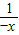=-（x+
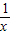）=-f（x），∴f（x）是奇函数
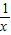+（-x）+（-
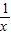）=0，∴f（x）=-f（-x），∴f（x）是奇函数
=
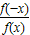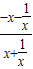=-1，∴f（-x）=-f（x），∴f（x）是奇函数
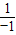=-2，又f（1）=1+
=2