题目内容
在5×5的棋盘中,放入3颗黑子和2颗白子,它们均不在同一行且不在同一列,则不同的排列方法种数为( )
| A.150 | B.200 | C.600 | D.1200 |
D
解析试题分析:如图 的棋盘中,
的棋盘中,
首先放入三颗黑子,在黑 黑 白 黑 白  的棋盘中,选出三行三列,共
的棋盘中,选出三行三列,共 种方法,然后放入三颗黑子,每一行放一颗黑子,共
种方法,然后放入三颗黑子,每一行放一颗黑子,共 种方法,然后在剩下的两行两列放两颗白子,共
种方法,然后在剩下的两行两列放两颗白子,共 种方法,所以不同的方法种数为
种方法,所以不同的方法种数为 种方法.故选D.
种方法.故选D.
考点:1.分步计数原理;2.排列组合的综合应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设 为整数
为整数 ,若
,若 和
和 被
被 除得的余数相同,则称
除得的余数相同,则称 和
和 对
对 同余记为
同余记为 ,已知
,已知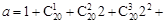 …
… ,
,  ,则
,则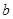 的值可以是
的值可以是
| A.2013 | B.2012 | C.2011 | D.2010 |
已知 的最小值是
的最小值是 ,则二项式
,则二项式 展开式中
展开式中 项的系数为( )
项的系数为( )
A. | B. | C. | D. |
高三要安排毕业晚会的4个音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求两个舞蹈节目不连排,则不同排法的种数是( )
| A.1800 | B.3600 | C.4320 | D.5040 |
如图所示,在连接正八边形的三个顶点而成的三角形中,与正八边形有公共边的三角形的个数为( )
| A.8 | B.32 | C.40 | D.48 |
用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( ).
| A.243 | B.252 | C.261 | D.279 |