题目内容
如图所示,三棱锥A-BCD中,AB⊥BC,AB⊥BD,BC⊥CD,且AB=BC=1.(1)求证:平面CBD⊥平面ABD;
(2)是否存在这样的三棱锥,使二面角C-AD-B的平面角为30°,如果存在,求出线段CD的长.如果不存在,请找出一个角q ,使得存在这样的三棱锥,也使二面角C—AD—B的平面角为q .
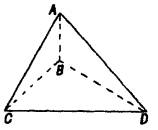
答案:
解析:
解析:
| 解:(1)如下图,证明:∵ ∴ (2)解:设 ∵ 平面 在平面 ∴ ∵ ∴ 不存在满足题意的三棱锥. 使二面角 ∵ 则
|

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ,若
,若 无解
无解
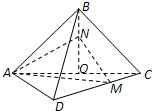 已知正方形ABCD的边长为2
已知正方形ABCD的边长为2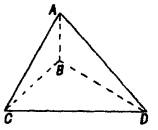
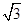 ,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为
,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为 
