题目内容
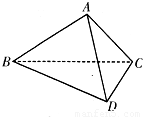
如图所示,在三棱锥A—BCD中,AB=3,AC=AD=2,且∠DAC=∠BAC=∠BAD=60°.求证:平面BCD⊥平面ADC.
证明:△ACD为正三角形,取CD中点M,连结AM、BM,△ABC≌△ABD,?
∴BC=BD.∴BM⊥CD,AM⊥CD.?
∵AM=![]() ,AB=3,cos60°=
,AB=3,cos60°=![]() ,?
,?
∴BC=![]() ,BM=
,BM=![]() .?
.?
∵BM2+AM2=AB2,?
∴BM⊥AM.?
∴BM⊥面ACD,且BM![]() 面BCD.?
面BCD.?
∴面ACD⊥面BCD.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
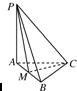 19、如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.
19、如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.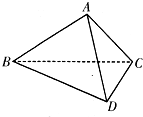 如图所示,在三棱锥A-BCD中,∠BDC为锐角,∠CBD=
如图所示,在三棱锥A-BCD中,∠BDC为锐角,∠CBD= 如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜
如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜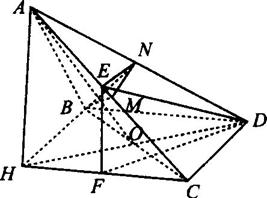
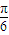 ,BC=
,BC=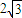 ,CD=AC=2,AB=AD=
,CD=AC=2,AB=AD=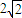 .
.