题目内容
在数列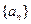 中,
中,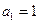 ,
,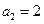 ,且
,且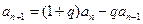 (
(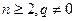 )。
)。
(Ⅰ)设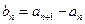 (
(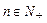 ),求数列
),求数列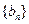 的通项公式;
的通项公式;
(Ⅱ)求数列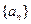 的通项公式。
的通项公式。
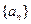 中,
中,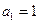 ,
,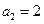 ,且
,且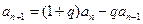 (
(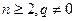 )。
)。(Ⅰ)设
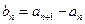 (
(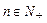 ),求数列
),求数列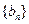 的通项公式;
的通项公式;(Ⅱ)求数列
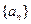 的通项公式。
的通项公式。(Ⅰ)
(Ⅱ)

(Ⅱ)

(Ⅰ)由题设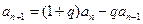 (
( ),得
),得 ,即
,即 ,
, 。又
。又 ,
, ,所以
,所以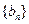 是首项为1,公比为
是首项为1,公比为 的等比数列,∴
的等比数列,∴ 。
。
(Ⅱ)由(Ⅰ)得 ,
,
 ,
,
……
 (
( )。
)。
将以上各式相加,得 (
( )。
)。
所以当 时,
时,
上式对 显然成立。
显然成立。
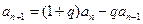 (
( ),得
),得 ,即
,即 ,
, 。又
。又 ,
, ,所以
,所以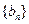 是首项为1,公比为
是首项为1,公比为 的等比数列,∴
的等比数列,∴ 。
。(Ⅱ)由(Ⅰ)得
 ,
, ,
,……
 (
( )。
)。将以上各式相加,得
 (
( )。
)。所以当
 时,
时,
上式对
 显然成立。
显然成立。
练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
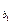 ,a
,a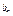 ,…,a
,…,a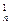 b1+C
b1+C b2+C
b2+C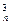 b3+…+C
b3+…+C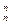 bn,求
bn,求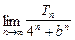 .
.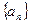 中,
中,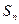 是其前
是其前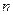 项和,且
项和,且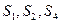 成等比数列.
成等比数列.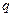 ;
;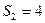 ,求等差数列
,求等差数列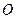 向三次曲线
向三次曲线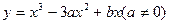 引切线,切于不同于点
引切线,切于不同于点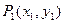 ,再由
,再由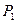 引此曲线的切线,切于不同于
引此曲线的切线,切于不同于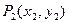 ,如此继续地作下去,……,得到点列
,如此继续地作下去,……,得到点列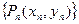 ,试回答下列问题: ⑴求
,试回答下列问题: ⑴求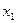 ; (2)求
; (2)求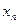 与
与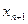 的关系式;
的关系式; 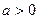 ,求证:当
,求证:当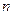 为正偶数时,
为正偶数时,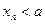 ;当
;当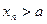 .
.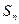 为等差数列
为等差数列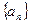 的前
的前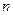 项和,
项和,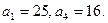
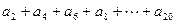 的值;
的值;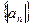 的前
的前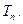
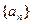 的前
的前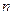 项和为
项和为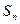 ,且
,且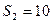 ,
,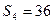 ,则过点
,则过点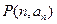 和
和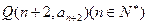 的直线的一个方向向量的坐标可以是( )
的直线的一个方向向量的坐标可以是( )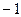 ,
,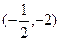

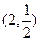
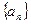 为等差数列,
为等差数列, (
(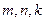 互不相等),求
互不相等),求 .
.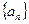 是首项为1的正项数列,且
是首项为1的正项数列,且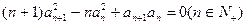 ,
,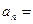 .
. 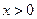 ,
,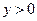 ,
,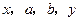 成等差数列,
成等差数列,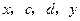 成等比数列,
成等比数列,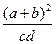 的最小值是( )
的最小值是( )