题目内容
在直角坐标平面内,定点F(-1,0)、F′(1,0),动点M,满足条件|| MF |
| MF′| |
| 2 |
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)过点F的直线交曲线C交于A,B两点,求以AB为直径的圆的方程,并判定这个圆与直线x=-2的位置关系.
分析:(Ⅰ)由题中条件:“|
|+|
=2
”易知M的轨迹是椭圆,结合椭圆的概念即可求得其方程;
(Ⅱ)分两种情形讨论:①当斜率存在时,设l:y=k(x+1),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系利用以AB为直径的圆的方程得到圆心到直线x=-2的距离d>R,所以圆于直线相离;当斜率不存在时,易得半径为
的圆与直线x=-2也相离,从而问题解决.
| MF |
| MF′| |
| 2 |
(Ⅱ)分两种情形讨论:①当斜率存在时,设l:y=k(x+1),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系利用以AB为直径的圆的方程得到圆心到直线x=-2的距离d>R,所以圆于直线相离;当斜率不存在时,易得半径为
| 1 | ||
|
解答:解:(Ⅰ)易知M的轨迹是椭圆,c=1,a=
,b=1,方程为
+y2=1.(3分)
(Ⅱ)①当斜率存在时,设l:y=k(x+1),由
,消去y整理得(1+2k2)x2+4k2x+2k2-2=0;(5分)
设A(x1,y1),B(x2,y2),则有
①(6分)
以AB为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0,
即x2+y2-(x1+x2)x-(y1+y2)y+x1x2+y1y2=0;②(7分)
由①得y1+y2=k(x1+1)+k(x2+1)=k(x1+x2)+2k=
,③y1y2=k2(x1+1)(x1+1)=k2[x1x2+(x1+x2)+1]=-
;④(8分)
将①③④代入②化简得x2+y2+
x-
y+
=0,
即(x+
)2+(y-
)2=[
]2.(10分)
对任意的k∈R,圆心(-
,
)到直线x=-2的距离是d=2-
=
,d-R=
-
=
>0,即d>R,所以圆于直线相离.(12分)
当斜率不存在时,易得半径为
,圆的方程是(x-1)2+y2=
,与直线x=-2也相离.(14分)
| 2 |
| x2 |
| 2 |
(Ⅱ)①当斜率存在时,设l:y=k(x+1),由
|
设A(x1,y1),B(x2,y2),则有
|
以AB为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0,
即x2+y2-(x1+x2)x-(y1+y2)y+x1x2+y1y2=0;②(7分)
由①得y1+y2=k(x1+1)+k(x2+1)=k(x1+x2)+2k=
| 2k |
| 1+2k2 |
| k2 |
| 1+2k2 |
将①③④代入②化简得x2+y2+
| 4k2 |
| 1+2k2 |
| 2k |
| 1+2k2 |
| k2-2 |
| 1+2k2 |
即(x+
| 2k2 |
| 1+2k2 |
| k |
| 1+2k2 |
| ||
| 1+2k2 |
对任意的k∈R,圆心(-
| 2k2 |
| 1+2k2 |
| k |
| 1+2k2 |
| 2k2 |
| 1+2k2 |
| 2k2+2 |
| 1+2k2 |
| 2k2+2 |
| 1+2k2 |
| ||
| 1+2k2 |
(2-
| ||
| 1+2k2 |
当斜率不存在时,易得半径为
| 1 | ||
|
| 1 |
| 2 |
点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
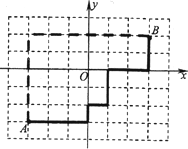
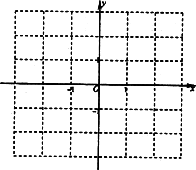


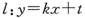 (k为常数)与正六边形交于M、N两点,记
(k为常数)与正六边形交于M、N两点,记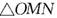 的面积为S,则关于函数
的面积为S,则关于函数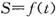 的奇偶性的判断正确的是 ( )
的奇偶性的判断正确的是 ( )