题目内容
已知函数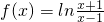 .
.
(Ⅰ) 求f(x)的反函数f-1(x);
(Ⅱ) 求不等式f(x)>0的解集;
(Ш) 讨论f(x)的单调性.
解:(Ⅰ) 由y=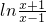 得ey=
得ey= .…(1分)
.…(1分)
xey-ey=x+1,…(2分)
xey-x=ey+1,即(ey-1)x=ey+1,…(3分)
∴x=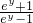 (y≠0).…(4分)
(y≠0).…(4分)
∴f-1(x)=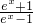 (x≠0)…(5分)
(x≠0)…(5分)
(Ⅱ)∵ >0,
>0,
∴x<-1或x>1.
所以,函数定义域为{x|x<-1或x>1}.…(6分)
根据题意,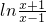 >0,即
>0,即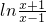 >ln1,…(7分)
>ln1,…(7分)
∴ >1.即
>1.即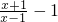 >0,也就是
>0,也就是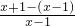 =
= >0,…(8分)
>0,…(8分)
∴x>1.…(9分)
所以,不等式f(x)>0的解集为{x|x>1}.…(10分)
(Ш)解法一:
设t= ,则y=lnt,x<-1或x>1.…(11分)
,则y=lnt,x<-1或x>1.…(11分)
t= =
=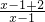 =1+
=1+ .…(12分)
.…(12分)
t= 向上平移1个单位得到t=
向上平移1个单位得到t= +1,再向右平移1个单位得到t=
+1,再向右平移1个单位得到t= ,t=1+
,t=1+ …(13分)
…(13分)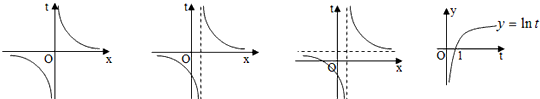
当x∈(-∞,-1)时,t是x的减函数,y是t的增函数; …(14分)
当x∈(1,+∞)时,t是x的减函数,y是t的增函数.…(15分)
所以,函数f(x)在(-∞,-1)和(1,+∞)上都是减函数.…(16分)
解法二:
设x1,x2是(1,+∞)上的任意两个实数,且x1<x1,…(11分)
则f(x1)-f(x2)=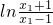 -
-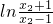 =
=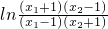 …(12分)
…(12分)
∵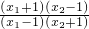 -1=
-1=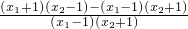 =
=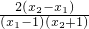 …(13分)
…(13分)
∵1<x1<x1,x2,
∴x2-x1>0,x1-1>0,x2+1>0.
∴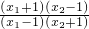 >1.…(14分)
>1.…(14分)
从而f(x1)-f(x2)=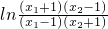 >ln1=0.即f(x1)>f(x2).
>ln1=0.即f(x1)>f(x2).
所以,函数f(x)在(1,+∞)上是减函数.…(15分)
同理,函数f(x)在(-∞,-1)上也是减函数.…(16分)
分析:(Ⅰ)由y=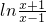 反解x=
反解x=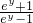 (y≠0),从而可求得f(x)的反函数f-1(x);
(y≠0),从而可求得f(x)的反函数f-1(x);
(Ⅱ)f(x)=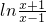 >0?
>0? >1(x|x<-1或x>1),解之即可.
>1(x|x<-1或x>1),解之即可.
(Ш)解法一:设t= ,则y=lnt,(x<-1或x>1),利用坐标变换,作出变换的图象,数形结合即可判断其单调性;
,则y=lnt,(x<-1或x>1),利用坐标变换,作出变换的图象,数形结合即可判断其单调性;
解法二:利用单调性的定义,设x1,x2是(1,+∞)上的任意两个实数,且x1<x1,作差f(x1)-f(x2),判断即可.
点评:本题考查反函数,考查函数单调性的判断与证明,考查解不等式,考查综合分析与运算能力、逻辑思维能力、创新能力,属于难题.
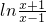 得ey=
得ey= .…(1分)
.…(1分)xey-ey=x+1,…(2分)
xey-x=ey+1,即(ey-1)x=ey+1,…(3分)
∴x=
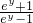 (y≠0).…(4分)
(y≠0).…(4分)∴f-1(x)=
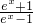 (x≠0)…(5分)
(x≠0)…(5分)(Ⅱ)∵
 >0,
>0,∴x<-1或x>1.
所以,函数定义域为{x|x<-1或x>1}.…(6分)
根据题意,
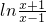 >0,即
>0,即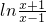 >ln1,…(7分)
>ln1,…(7分)∴
 >1.即
>1.即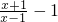 >0,也就是
>0,也就是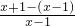 =
= >0,…(8分)
>0,…(8分)∴x>1.…(9分)
所以,不等式f(x)>0的解集为{x|x>1}.…(10分)
(Ш)解法一:
设t=
 ,则y=lnt,x<-1或x>1.…(11分)
,则y=lnt,x<-1或x>1.…(11分)t=
 =
=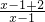 =1+
=1+ .…(12分)
.…(12分)t=
 向上平移1个单位得到t=
向上平移1个单位得到t= +1,再向右平移1个单位得到t=
+1,再向右平移1个单位得到t= ,t=1+
,t=1+ …(13分)
…(13分)
当x∈(-∞,-1)时,t是x的减函数,y是t的增函数; …(14分)
当x∈(1,+∞)时,t是x的减函数,y是t的增函数.…(15分)
所以,函数f(x)在(-∞,-1)和(1,+∞)上都是减函数.…(16分)
解法二:
设x1,x2是(1,+∞)上的任意两个实数,且x1<x1,…(11分)
则f(x1)-f(x2)=
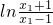 -
-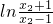 =
=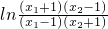 …(12分)
…(12分)∵
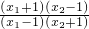 -1=
-1=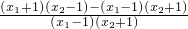 =
=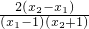 …(13分)
…(13分)∵1<x1<x1,x2,
∴x2-x1>0,x1-1>0,x2+1>0.
∴
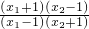 >1.…(14分)
>1.…(14分)从而f(x1)-f(x2)=
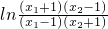 >ln1=0.即f(x1)>f(x2).
>ln1=0.即f(x1)>f(x2).所以,函数f(x)在(1,+∞)上是减函数.…(15分)
同理,函数f(x)在(-∞,-1)上也是减函数.…(16分)
分析:(Ⅰ)由y=
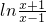 反解x=
反解x=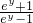 (y≠0),从而可求得f(x)的反函数f-1(x);
(y≠0),从而可求得f(x)的反函数f-1(x);(Ⅱ)f(x)=
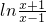 >0?
>0? >1(x|x<-1或x>1),解之即可.
>1(x|x<-1或x>1),解之即可.(Ш)解法一:设t=
 ,则y=lnt,(x<-1或x>1),利用坐标变换,作出变换的图象,数形结合即可判断其单调性;
,则y=lnt,(x<-1或x>1),利用坐标变换,作出变换的图象,数形结合即可判断其单调性;解法二:利用单调性的定义,设x1,x2是(1,+∞)上的任意两个实数,且x1<x1,作差f(x1)-f(x2),判断即可.
点评:本题考查反函数,考查函数单调性的判断与证明,考查解不等式,考查综合分析与运算能力、逻辑思维能力、创新能力,属于难题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
. 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求