题目内容
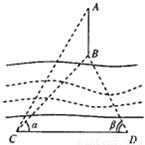
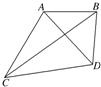 如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.
如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.分析:先根据,∠ACD=60°,∠ADC=60°判断出△ACD为正三角形,进而求得AC,进而在△BCD中,由正弦定理可求得BC,最后在△ABC中,利用余弦定理即可求得AB.
解答:解:在△ACD中,已知CD=a,∠ACD=60°,∠ADC=60°,所以AC=a.①
在△BCD中,由正弦定理可得
BC=
=
a.②
在△ABC中,已经求得AC和BC,又因为∠ACB=30°,
所以利用余弦定理可以求得A、B两点之间的距离为
AB=
=
a.
在△BCD中,由正弦定理可得
BC=
| asin105° |
| sin45° |
| ||
| 2 |
在△ABC中,已经求得AC和BC,又因为∠ACB=30°,
所以利用余弦定理可以求得A、B两点之间的距离为
AB=
| AC2+BC2-2AC•BC•cos30° |
| ||
| 2 |
点评:本题主要考查了解三角形的实际应用.注意灵活利用正弦定理和余弦定理及其变形公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
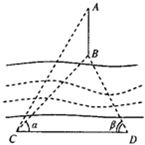 如图所示,为了测量河对岸地面上A,B两点间的距离,某人在河岸边上选取了C,D两点,使得CD⊥AB,且CD=500(米)现测得∠BCD=α,∠BDC=β,∠ACD=60°,其中cosα=
如图所示,为了测量河对岸地面上A,B两点间的距离,某人在河岸边上选取了C,D两点,使得CD⊥AB,且CD=500(米)现测得∠BCD=α,∠BDC=β,∠ACD=60°,其中cosα=
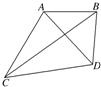 如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.
如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长. ,tanβ=2.求:
,tanβ=2.求: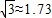 )
)