题目内容
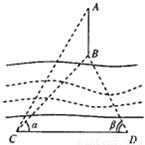
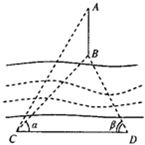 如图所示,为了测量河对岸地面上A,B两点间的距离,某人在河岸边上选取了C,D两点,使得CD⊥AB,且CD=500(米)现测得∠BCD=α,∠BDC=β,∠ACD=60°,其中cosα=
如图所示,为了测量河对岸地面上A,B两点间的距离,某人在河岸边上选取了C,D两点,使得CD⊥AB,且CD=500(米)现测得∠BCD=α,∠BDC=β,∠ACD=60°,其中cosα=| 3 |
| 5 |
(1)sin∠CBD的值;
(2)A,B两点间的距离(精确到1米).(参考数据
| 3 |
分析:(1)由α+β+∠CBD=π,得sin∠CBD=sin(α+β),知cosα可求sinα,知tanβ,用同角三角函数的基本关系,可求sinβ,cosβ.
(2)在△BCD中,用正弦定理求出BC,在△ABC中求出sin∠ACB,再利用正弦定理求AB.
(2)在△BCD中,用正弦定理求出BC,在△ABC中求出sin∠ACB,再利用正弦定理求AB.
解答:解:(1)∵cosα=
,α为锐角,∴sinα=
∵tanβ=2,β锐角,∴sinβ=
,cosβ=
(3分)
sin∠CBD=sin(α+β)=sinαcosβ+cosαsinβ=
×
+
×
=
(5分)
(2)在△BCD中,由
=
得BC=sinD•
=
•
=500(7分)
∴sin∠ACB=sin(600-α)=
×
-
×
=
(9分)
由AB⊥CD,∠ACD=60°,得∠A=30°(11分)
△ABC中,由
=
,
得AB=sin∠ACB×
=
×
=300
-400≈119(米),
答:A、B两点间距离约为119米.
| 3 |
| 5 |
| 4 |
| 5 |
∵tanβ=2,β锐角,∴sinβ=
| 2 | ||
|
| 1 | ||
|
sin∠CBD=sin(α+β)=sinαcosβ+cosαsinβ=
| 4 |
| 5 |
| 1 | ||
|
| 3 |
| 5 |
| 2 | ||
|
2
| ||
| 5 |
(2)在△BCD中,由
| BC |
| sinD |
| CD |
| sin∠CBD |
| CD |
| sin∠CBD |
| 2 | ||
|
| 500 | ||||
|
∴sin∠ACB=sin(600-α)=
| ||
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
3
| ||
| 10 |
由AB⊥CD,∠ACD=60°,得∠A=30°(11分)
△ABC中,由
| AB |
| sin∠ACB |
| BC |
| sinA |
得AB=sin∠ACB×
| BC |
| sinA |
3
| ||
| 10 |
| 500 | ||
|
| 3 |
答:A、B两点间距离约为119米.
点评:本题考查解三角形的实际应用,用到两角和的正弦公式,正弦定理等知识,正弦定理在解三角形时,用于下面两种情况:一是知两边一对角,二是知两角和一边.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
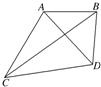 如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.
如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.
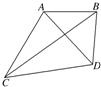 如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.
如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长. ,tanβ=2.求:
,tanβ=2.求: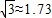 )
)