题目内容
已知椭圆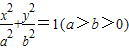
的左、右焦点分别为F1（-c，0），F2（c，0），若椭圆上存在一点P使
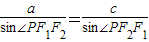，则该椭圆的离心率的取值范围为 ．
【答案】分析：由“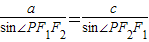
”的结构特征，联想到在△PF1F2中运用由正弦定理得：
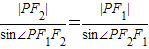两者结合起来，可得到
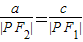，再由焦点半径公式，代入可得到：a（a+ex）=c（a-ex）解出x，由椭圆的范围，建立关于离心率的不等式求解．要注意椭圆离心率的范围．
解答：解：在△PF1F2中，
由正弦定理得：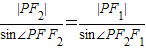
则由已知得：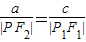
，
即：a|PF1|=c|PF2|
设点（x，y）由焦点半径公式，
得：|PF1|=a+ex，|PF2|=a-ex
则a（a+ex）=c（a-ex）
解得：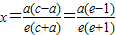
由椭圆的几何性质知：x＞-a则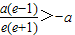
，
整理得e2+2e-1＞0，解得：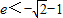
或
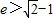，又e∈（0，1），
故椭圆的离心率：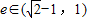
，
故答案为：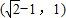
．
点评：本题主要考查椭圆的定义，性质及焦点三角形的应用，特别是离心率应是椭圆考查的一个亮点，多数是用a，b，c转化，用椭圆的范围来求解离心率的范围．
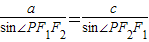”的结构特征，联想到在△PF1F2中运用由正弦定理得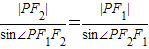：两者结合起来，可得到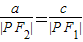，再由焦点半径公式，代入可得到：a（a+ex）=c（a-ex）解出x，由椭圆的范围，建立关于离心率的不等式求解．要注意椭圆离心率的范围．解答：解：在△PF1F2中，
由正弦定理得：
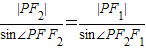
则由已知得：
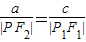，即：a|PF1|=c|PF2|
设点（x，y）由焦点半径公式，
得：|PF1|=a+ex，|PF2|=a-ex
则a（a+ex）=c（a-ex）
解得：
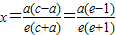
由椭圆的几何性质知：x＞-a则
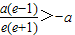，整理得e2+2e-1＞0，解得：
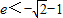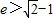或，又e∈（0，1），故椭圆的离心率：
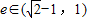，故答案为：
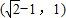．点评：本题主要考查椭圆的定义，性质及焦点三角形的应用，特别是离心率应是椭圆考查的一个亮点，多数是用a，b，c转化，用椭圆的范围来求解离心率的范围．
练习册系列答案
相关题目
的左、右焦点分别为
，其右准线上
上存在点
（点
轴上方），使
为等腰三角形．
的范围；
到两焦点
，求
的左、右焦点分别为
，
，
点
是椭圆的一个顶点，△
是等腰直角三角形．
分别作直线
，
交椭圆于
，
两点，设两直线的斜率分别为
，
，且
，证明：直线
过定点（
）．
的左、右焦点分别为F1、F2，其中
的焦点，M是C1与C2在第一象限的交点，且
上，求直线AC的方程。
的左、右焦点分别为
、
，离心率
，右准线方程为
．
与该椭圆交于M、N两点，且
，求直线