题目内容
【题目】
函数
是定义在
上的奇函数，且
。
（1）求实数a，b，并确定函数
的解析式；
（2）判断在（-1，1）上的单调性，并用定义证明你的结论；
（3）写出的单调减区间，并判断有无最大值或最小值？如有，写出最大值或最小值。（本小问不需要说明理由）
【答案】（1）
（2）见解析（3）单调减区间为
x=-1时，
，当x=1时，
。
【解析】
试题（1）先根据函数为奇函数（
）求出
值，再利用
求出
值，即可其解析式；（2）利用函数的单调性定义进行判定与证明；（3）结合（2）问容易得到单调递减区间，进而写出最值.
解题思路:（1）求解析式的一种主要方法是待定系数法；（2）利用函数单调性的定义证明函数的单调性的一般步骤为：设值代值、作差变形、判定符号、下结论.
试题解析：（1）
是奇函数，
。
即
，
，
，又，
，
，
（2）任取
，且
，
，
，
，
，
，
在（-1，1）上是增函数。
（3）单调减区间为
当x=-1时，，当x=1时，
.
快乐5加2金卷系列答案
【题目】某葡萄基地的种植专家发现，葡萄每株的收获量
（单位： 
）和与它“相近”葡萄的株数
具有线性相关关系（所谓两株作物“相近”是指它们的直线距离不超过
），并分别记录了相近葡萄的株数为1,2,3,4,5,6,7时，该葡萄每株收获量的相关数据如下：
| 1 | 2 | 3 | 5 | 6 | 7 |
| 15 | 13 | 12 | 10 | 9 | 7 |
（1）求该葡萄每株的收获量
关于它“相近”葡萄的株数
的线性回归方程及
的方差
；
（2）某葡萄专业种植户种植了1000株葡萄，每株“相近”的葡萄株数按2株计算，当年的葡萄价格按10元/ 
投入市场，利用上述回归方程估算该专业户的经济收入为多少万元；（精确到0.01）
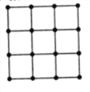
（3）该葡萄基地在如图所示的正方形地块的每个格点（指纵、横直线的交叉点）处都种了一株葡萄，其中每个小正方形的面积都为
，现在所种葡萄中随机选取一株，求它的收获量的分布列与数学期望.（注：每株收获量以线性回归方程计算所得数据四舍五入后取的整数为依据）
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名，其中每天玩微信超过6小时的用户列为“微信控”，否则称其为“非微信控”，调查结果如下：
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
（1）根据以上数据，能否有95%的把握认为“微信控”与“性别”有关？
（2）现从调查的女性用户中按分层抽样的方法选出5人，再随机抽取3人赠送礼品，记这3人中“微信控”的人数为
，试求
的分布列和数学期望.
参考公式: 
，其中
.
参考数据：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
