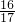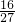题目内容
若x、y∈R+，3x+y=3，则xy的最大值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
分析：首先由题意由3x+y=3，求xy的最大值，可以联想到用基本不等式求解，根据a+b≥2
，应用到等式3x+y=3中直接求解，即可得到答案．
| ab |
解答：解：因为3x+y=3根据基本不等式a+b≥2
所以3x+y=3≥2
，得到xy≤
故选C．
| ab |
所以3x+y=3≥2
| 3xy |
| 3 |
| 4 |
故选C．
点评：此题主要考查基本不等式a+b≥2
的应用问题，在求函数最大值最小值的问题中，基本不等式应用广泛，需要理解记忆．
| ab |
练习册系列答案
相关题目
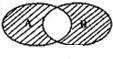如图所示的韦恩图中，A、B是非空集合，定义A*B表示阴影部分的集合．若x，y∈R，A={x|y=
（2013•牡丹江一模）如图所示的韦恩图中，A、B是非空集合，定义A*B表示阴影部分集合．若x，y∈R，
