Question

【题目】已知函数（其中）．

（1）当时，求零点的个数k的值；

（2）在（1）的条件下，记这些零点分别为，求证： ．

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】试题分析：（1）利用导数研究函数的单调性，可得当x＞时， ， 为增函数；当时， ， 为减函数，所以，判断出、、； 的符号，结合函数图象，利用零点定理可得结果；（2）由（1）知的两个零点为，不妨设， 可得，进而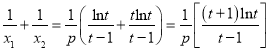， ，只需利用导数证明即可得结论.

试题解析：（1）由题x＞0， ，则，

由得，

当x＞时， ， 为增函数；当0<x< 时， ， 为减函数，

所以．

因为，所以，

而

，又，

所以当时， 零点的个数为2．

（2）由（1）知的两个零点为，不妨设，

于是且，

两式相减得（*）， 令，

则将代入（*）得，进而，

所以，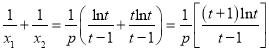

下面证明，其中，

即证明，设，

则，令 ，则，

所以为增函数，即为增函数，

故，故为减函数，

于是，即．

所以有，从而．而由，得，

所以，得证．