题目内容

平面内A、B、C为l上的三个定点,AB=2,BC=1,动点Pl,且恒有∠APB=∠BPC.

(1)求动点P的轨迹方程.

(2)若曲线F:y2=a(x+1)(a＞0)与P的轨迹仅有两个交点,求a的值.

解：(1)以B为原点,直线l为x轴建立直角坐标系,

设P(x,y)、A(-2,0)、C(1,0)、B(0,0),

由Pl,∠APB=∠BPC得==2,

所以=2,

整理得x2+y2-4x=0(y≠0),这即是所求P点的轨迹方程.

(2)曲线F与P点的轨迹仅有两个交点的充要条件是:

方程组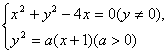有两组不同的实数解,所以方程x2+(a-4)x+a=0(a＞0)只有两个相同的正数解.

因此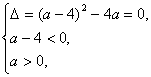

解得a=6-2.

练习册系列答案
相关题目
下列命题中，错误命题的序号有
 
．
（1）“a=-1”是“函数f（x）=x2+|x+a+1|（ x∈R） 为偶函数”的必要条件；
（2）“直线l垂直平面α内无数条直线”是“直线l垂直平面α”的充分条件；
（3）已知a，b，c为非零向量，则“a•b=a•c”是“b=c”的充要条件；
（4）若p：?x∈R，x2+2x+2≤0，则￢p：?x∈R，x2+2x+2＞0．
下面四个命题中,真命题的个数为(    )

①如果两个平面有三个公共点,那么这两个平面重合;②两条直线可以确定一个平面;③若M∈α,M∈β,α∩β=l,则M∈l;④空间中,相交于同一点的三条直线在同一平面内.

A.1                  B.2                   C.3                 D.4

下列命题中，错误命题的序号有______．
（1）“a=-1”是“函数f（x）=x2+|x+a+1|（ x∈R） 为偶函数”的必要条件；
（2）“直线l垂直平面α内无数条直线”是“直线l垂直平面α”的充分条件；
（3）已知a，b，c为非零向量，则“a•b=a•c”是“b=c”的充要条件；
（4）若p：?x∈R，x2+2x+2≤0，则￢p：?x∈R，x2+2x+2＞0．
下列命题中，错误命题的序号有    ．
（1）“a=-1”是“函数f（x）=x2+|x+a+1|（ x∈R） 为偶函数”的必要条件；
（2）“直线l垂直平面α内无数条直线”是“直线l垂直平面α”的充分条件；
（3）已知a，b，c为非零向量，则“a•b=a•c”是“b=c”的充要条件；
（4）若p：?x∈R，x2+2x+2≤0，则￢p：?x∈R，x2+2x+2＞0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网