题目内容
抛物线C的顶点在原点,焦点F与双曲线
-
=1的右焦点重合,过点P(2,0)且斜率为1的直线l与抛物线C交于A、B两点.
(1)求弦长|AB|;
(2)求弦AB中点到抛物线准线的距离.
| x2 |
| 3 |
| y2 |
| 6 |
(1)求弦长|AB|;
(2)求弦AB中点到抛物线准线的距离.
分析:(1)由题意可得F(3,0),从而可得抛物线的方程,及过点P得直线方程,联立方程
可得x2-16x+4=0
AB=
,根据方程的根与系数的关系代入即可求解
(2)设AB得中点为M(x0,y0),分别过点AMB做准线的垂线,垂足分别为A′,M′,B′,由梯形得性质可得,MM′=
(AA′+BB′)=(x1+3+x2+3)×
,结合(1)可求
|
AB=
| 2[(x1+x2)2-4x1x2 ] |
(2)设AB得中点为M(x0,y0),分别过点AMB做准线的垂线,垂足分别为A′,M′,B′,由梯形得性质可得,MM′=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)由题意可得双曲线的右焦点(3,0),故F(3,0)
∴抛物线的方程为y2=12x,过点P得直线方程为y=x-2
联立方程
可得x2-16x+4=0设A(x1,y1)B(x2,y2)
则x1+x2=16,x1x2=4
AB=
=
=4
(2)设AB得中点为M(x0,y0)
分别过点AMB做准线的垂线,垂足分别为A′,M′,B′,
则由梯形得性质可得,MM′=
(AA′+BB′)=(x1+3+x2+3)×
=
× 22=11
∴抛物线的方程为y2=12x,过点P得直线方程为y=x-2
联立方程
|
则x1+x2=16,x1x2=4
AB=
| 2[(x1+x2)2-4x1x2 ] |
| 2(256-16) |
| 30 |
(2)设AB得中点为M(x0,y0)
分别过点AMB做准线的垂线,垂足分别为A′,M′,B′,
则由梯形得性质可得,MM′=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了由抛物线的性质求解抛物线的方程,关键是看清题中给出的条件,灵活运用方程的根与系数的关系及弦长公式AB=
进行求解.
| 2[(x1+x2)2-4x1x2 ] |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
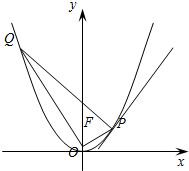 已知抛物线C的顶点在原点,焦点为F(0,1).
已知抛物线C的顶点在原点,焦点为F(0,1). 已知抛物线C的顶点在原点,焦点坐标为F(2,0),点P的坐标为(m,0)(m≠0),设过点P的直线l交抛物线C于A,B两点,点P关于原点的对称点为点Q.
已知抛物线C的顶点在原点,焦点坐标为F(2,0),点P的坐标为(m,0)(m≠0),设过点P的直线l交抛物线C于A,B两点,点P关于原点的对称点为点Q.