题目内容
 在四棱锥P-ABCD中,AD⊥AB,CD∥AB∥MN,PD⊥底面ABCD,
在四棱锥P-ABCD中,AD⊥AB,CD∥AB∥MN,PD⊥底面ABCD,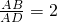 ,直线PA与底面ABCD成60°角,点M,N分别是PA、PB的中点.
,直线PA与底面ABCD成60°角,点M,N分别是PA、PB的中点.
(Ⅰ)求二面角P-MN-D的大小;
(Ⅱ)当 的值为多少时,∠CND为直角?
的值为多少时,∠CND为直角?
解:(Ⅰ)∵PD⊥面ABCD,AB?面ABCD,
∴AB⊥PD,又AB⊥AD,∴AB⊥面PAD.
又MN是△PAB的中位线,∴MN∥AB,从而MN⊥面PAD,
∴∠PMD为二面角P-MN-D的平面角,
由已知,在Rt△PAD中,易证:∠PAD=60°,而M是PA的中点,
∴∠PMD=120°.
即所求二面角P-MN-D的大小为120°.
 (Ⅱ)令
(Ⅱ)令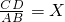 ,不妨设AD=2,则
,不妨设AD=2,则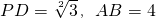 ,CD=X,AB=4X.
,CD=X,AB=4X.
以D为原点,DA、DC、DP所在直线分别为x、y、z轴建立空间直角坐标系,则
D(0,0,0),N(1,2, ),C(0,4x,0),
),C(0,4x,0),
∴ (1,2,
(1,2, ),
),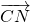 (1,2-4x,
(1,2-4x, ),
),
若∠CND为直角,则必有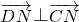 ,
,
即
于是有 ,解得x=1.
,解得x=1.
∴当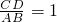 时,∠CND为直角.
时,∠CND为直角.
分析:(I)由题意利用线面垂直的判定定理,得到线面垂直,在利用二面角的概念得到二面角的平面角即可得;
(II)由题意利用题中的条件及图形建立空间直角坐标系,设出比例值为x,利用空间向量的知识建立未知量的方程进而求解.
点评:此题重点考查了学生的空间想象能力,线面垂直的判定,利用二面角的概念求出二面角的平面角比求出二面角的大小;此外还考查了利用空间向量的知识及方程的思想求解.
∴AB⊥PD,又AB⊥AD,∴AB⊥面PAD.
又MN是△PAB的中位线,∴MN∥AB,从而MN⊥面PAD,
∴∠PMD为二面角P-MN-D的平面角,
由已知,在Rt△PAD中,易证:∠PAD=60°,而M是PA的中点,
∴∠PMD=120°.
即所求二面角P-MN-D的大小为120°.
 (Ⅱ)令
(Ⅱ)令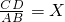 ,不妨设AD=2,则
,不妨设AD=2,则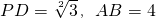 ,CD=X,AB=4X.
,CD=X,AB=4X.以D为原点,DA、DC、DP所在直线分别为x、y、z轴建立空间直角坐标系,则
D(0,0,0),N(1,2,
 ),C(0,4x,0),
),C(0,4x,0),∴
 (1,2,
(1,2, ),
),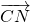 (1,2-4x,
(1,2-4x, ),
),若∠CND为直角,则必有
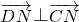 ,
,即

于是有
 ,解得x=1.
,解得x=1.∴当
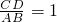 时,∠CND为直角.
时,∠CND为直角.分析:(I)由题意利用线面垂直的判定定理,得到线面垂直,在利用二面角的概念得到二面角的平面角即可得;
(II)由题意利用题中的条件及图形建立空间直角坐标系,设出比例值为x,利用空间向量的知识建立未知量的方程进而求解.
点评:此题重点考查了学生的空间想象能力,线面垂直的判定,利用二面角的概念求出二面角的平面角比求出二面角的大小;此外还考查了利用空间向量的知识及方程的思想求解.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,