题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() (
(![]() ).点
).点![]() 在
在![]() 上,
上,![]() ,△
,△![]() 的周长为
的周长为![]() ,面积为
,面积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切,求直线
相切,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)依题意知△![]() 的周长为
的周长为![]() ,得
,得![]() ,又由△
,又由△![]() 的面积
的面积![]() ,求得
,求得![]() ,得出
,得出![]() ,联立方程组,求得
,联立方程组,求得![]() 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,联立方程组,利用根与系数的关系,求得
,联立方程组,利用根与系数的关系,求得![]() ,再由弦长公式得
,再由弦长公式得![]() ,得出以
,得出以![]() 为直径的圆的圆心坐标与半径,再利用圆
为直径的圆的圆心坐标与半径,再利用圆![]() 与直线
与直线![]() 相切,解得
相切,解得![]() ,即可得到答案.
,即可得到答案.
(1)设椭圆![]() ,
,
依题意知△![]() 的周长为
的周长为![]() ,得
,得![]() ,…①
,…①
又因为![]() ,所以
,所以![]() ,
,
所以△![]() 的面积
的面积![]() ,
,
所以![]() ,即
,即![]() …②,
…②,
联立①②解得![]() ,则
,则![]() ,
,
所以![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 斜率为0时,不满足题意.
斜率为0时,不满足题意.
设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
由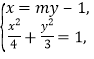 消去
消去![]() ,得
,得![]() ,
,
从而![]() ,
,
所以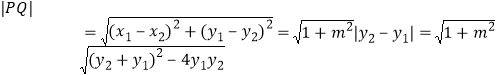
![]()
![]() ,
,
设以![]() 为直径的圆的圆心
为直径的圆的圆心![]() ,半径为
,半径为![]() ,则
,则![]() ,
,
又![]() ,
,![]() ,
,
又因为圆![]() 与直线
与直线![]() 相切,则
相切,则![]() ,即
,即![]() ,解得
,解得![]() .
.
所以直线![]() 的方程为
的方程为![]() ,即
,即![]()

【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 垂直于
垂直于![]() 轴的直线与抛物线
轴的直线与抛物线![]() 相交于
相交于![]() 两点,抛物线
两点,抛物线![]() 在
在![]() 两点处的切线及直线
两点处的切线及直线![]() 所围成的三角形面积为
所围成的三角形面积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设![]() 是抛物线
是抛物线![]() 上异于原点
上异于原点![]() 的两个动点,且满足
的两个动点,且满足![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
【题目】某新上市的电子产品举行为期一个星期(7天)的促销活动,规定购买该电子产品可免费赠送礼品一份,随着促销活动的有效开展,第五天工作人员对前五天中参加活动的人数进行统计,![]() 表示第
表示第![]() 天参加该活动的人数,得到统计表格如下:
天参加该活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 6 | 10 | 23 | 22 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)预测该星期最后一天参加该活动的人数(按四舍五入取到整数).
参考公式: ,
,![]()
【题目】某新上市的电子产品举行为期一个星期(7天)的促销活动,规定购买该电子产品可免费赠送礼品一份,随着促销活动的有效开展,第五天工作人员对前五天中参加活动的人数进行统计,y表示第x天参加该活动的人数,得到统计表格如下,经计算得![]() .
.
x | 1 | 2 | 3 | 4 | 5 |
y | 4 | m | 10 | 23 | 22 |
(1)若y与x具有线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)预测该星期最后一天参加该活动的人数(按四舍五入取到整数).
参考公式:
 ,
,![]()