题目内容
已知函数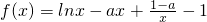 (a∈R).
(a∈R).
(Ⅰ) 当a≥0时,讨论f(x)的单调性;
(Ⅱ)设g(x)=x2-2bx+4.当 时,
时,
(i)若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数b取值范围.
(ii) 对于任意x1,x2∈(1,2]都有 ,求λ的取值范围.
,求λ的取值范围.
解:(Ⅰ)函数f(x)的定义域为(0,+∞),
因为 ,
,
所以当a=0时,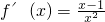 ,令
,令 得x>1,
得x>1,
所以此时函数f(x)在(1,+∞)上是增函数,在(0,1)是减函数;-----------------------------(2分)
当 时,
时, ,所以此时函数f(x)在(0,+∞)是减函数;
,所以此时函数f(x)在(0,+∞)是减函数;
当 时,令
时,令 ,解得
,解得 ,
,
此时函数f(x)在 是增函数,在
是增函数,在 上是减函数;----------------------------------------------(4分)
上是减函数;----------------------------------------------(4分)
当 ,令
,令 ,解得
,解得 ,
,
此时函数f(x)在 是增函数,在
是增函数,在 上是减函数;-----------------------------------------(6分)
上是减函数;-----------------------------------------(6分)
当a≥1,由于 ,令
,令 ,解得0<x<1,
,解得0<x<1,
此时函数f(x)在(0,1)是增函数,在(1,+∞)上是减函数.--------------------------------------------(8分)
(Ⅱ) (i)当 时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,所以对任意x1∈(0,2),
时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,所以对任意x1∈(0,2),
有 ,又已知存在x2∈[1,2],使f(x1)≥g(x2),所以
,又已知存在x2∈[1,2],使f(x1)≥g(x2),所以 ,x2∈[1,2],
,x2∈[1,2],
即存在x∈[1,2],使 ,即
,即 ,即
,即
 ,
,
所以 ,解得
,解得 ,即实数b取值范围是
,即实数b取值范围是 .--------------------(12分)
.--------------------(12分)
(ii)不妨设1<x1≤x2≤2,由函数f(x)在(1,2]上是增函数,函数 在(1,2]是减函数,
在(1,2]是减函数,
∴ 等价于
等价于 ,
,
所以
设 是减函数,
是减函数,
所以h'(x)≤0在(1,2]上恒成立,即 ,解得
,解得 .---------(16分)
.---------(16分)
分析:(I)由已知中函数的意义域为R+,由已知中的函数解析式,求出导函数的解析式,分a=0, ,
, ,
, ,a≥1五种情况分别讨论,最后综合讨论结果,即可得到f(x)的单调性;
,a≥1五种情况分别讨论,最后综合讨论结果,即可得到f(x)的单调性;
(Ⅱ)(i)由(I)的结论,我们可得当 时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,则f(x1)≥g(x2),可转化为
时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,则f(x1)≥g(x2),可转化为 ≥f(x2),由g(x)=x2-2bx+4,我们易由函数恒成立问题的处理方法,求出满足条件的实数b取值范围.
≥f(x2),由g(x)=x2-2bx+4,我们易由函数恒成立问题的处理方法,求出满足条件的实数b取值范围.
(ii) 由(I)中结论函数f(x)在(1,2]上是增函数,函数 在(1,2]是减函数,则
在(1,2]是减函数,则 等价于
等价于 ,构造函数
,构造函数 ,可得函数h(x)是减函数,根据h'(x)≤0在(1,2]上恒成立,可构造关于λ的不等式,解不等式即可得到答案.
,可得函数h(x)是减函数,根据h'(x)≤0在(1,2]上恒成立,可构造关于λ的不等式,解不等式即可得到答案.
点评:本题考查的知识点是利用导数研究函数的单调性,函数恒成立问题,其中(1)的关键是对a值进行分类讨论,而(2)的关键是构造函数 ,进而根据函数h(x)是减函数,则h'(x)≤0在(1,2]上恒成立,构造关于λ的不等式.
,进而根据函数h(x)是减函数,则h'(x)≤0在(1,2]上恒成立,构造关于λ的不等式.
因为
 ,
,所以当a=0时,
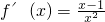 ,令
,令 得x>1,
得x>1,所以此时函数f(x)在(1,+∞)上是增函数,在(0,1)是减函数;-----------------------------(2分)
当
 时,
时, ,所以此时函数f(x)在(0,+∞)是减函数;
,所以此时函数f(x)在(0,+∞)是减函数;当
 时,令
时,令 ,解得
,解得 ,
,此时函数f(x)在
 是增函数,在
是增函数,在 上是减函数;----------------------------------------------(4分)
上是减函数;----------------------------------------------(4分)当
 ,令
,令 ,解得
,解得 ,
,此时函数f(x)在
 是增函数,在
是增函数,在 上是减函数;-----------------------------------------(6分)
上是减函数;-----------------------------------------(6分)当a≥1,由于
 ,令
,令 ,解得0<x<1,
,解得0<x<1,此时函数f(x)在(0,1)是增函数,在(1,+∞)上是减函数.--------------------------------------------(8分)
(Ⅱ) (i)当
 时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,所以对任意x1∈(0,2),
时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,所以对任意x1∈(0,2),有
 ,又已知存在x2∈[1,2],使f(x1)≥g(x2),所以
,又已知存在x2∈[1,2],使f(x1)≥g(x2),所以 ,x2∈[1,2],
,x2∈[1,2],即存在x∈[1,2],使
 ,即
,即 ,即
,即
 ,
,所以
 ,解得
,解得 ,即实数b取值范围是
,即实数b取值范围是 .--------------------(12分)
.--------------------(12分)(ii)不妨设1<x1≤x2≤2,由函数f(x)在(1,2]上是增函数,函数
 在(1,2]是减函数,
在(1,2]是减函数,∴
 等价于
等价于 ,
,所以

设
 是减函数,
是减函数,所以h'(x)≤0在(1,2]上恒成立,即
 ,解得
,解得 .---------(16分)
.---------(16分)分析:(I)由已知中函数的意义域为R+,由已知中的函数解析式,求出导函数的解析式,分a=0,
 ,
, ,
, ,a≥1五种情况分别讨论,最后综合讨论结果,即可得到f(x)的单调性;
,a≥1五种情况分别讨论,最后综合讨论结果,即可得到f(x)的单调性;(Ⅱ)(i)由(I)的结论,我们可得当
 时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,则f(x1)≥g(x2),可转化为
时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,则f(x1)≥g(x2),可转化为 ≥f(x2),由g(x)=x2-2bx+4,我们易由函数恒成立问题的处理方法,求出满足条件的实数b取值范围.
≥f(x2),由g(x)=x2-2bx+4,我们易由函数恒成立问题的处理方法,求出满足条件的实数b取值范围.(ii) 由(I)中结论函数f(x)在(1,2]上是增函数,函数
 在(1,2]是减函数,则
在(1,2]是减函数,则 等价于
等价于 ,构造函数
,构造函数 ,可得函数h(x)是减函数,根据h'(x)≤0在(1,2]上恒成立,可构造关于λ的不等式,解不等式即可得到答案.
,可得函数h(x)是减函数,根据h'(x)≤0在(1,2]上恒成立,可构造关于λ的不等式,解不等式即可得到答案.点评:本题考查的知识点是利用导数研究函数的单调性,函数恒成立问题,其中(1)的关键是对a值进行分类讨论,而(2)的关键是构造函数
 ,进而根据函数h(x)是减函数,则h'(x)≤0在(1,2]上恒成立,构造关于λ的不等式.
,进而根据函数h(x)是减函数,则h'(x)≤0在(1,2]上恒成立,构造关于λ的不等式. 
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).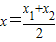 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.