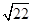题目内容
在三角形中,A、B、C分别是三内角,有: 。则类比可得
。则类比可得
A、 B、
B、
C、 D、以上都不对
D、以上都不对
B
解析试题分析:三角形中,A、B、C分别是三内角,有: ,则根据余弦函数可知,类比可得
,则根据余弦函数可知,类比可得 ,成立,故选B.
,成立,故选B.
考点:解三角形
点评:主要是考查了正弦定理的运用,属于基础题。

练习册系列答案
相关题目
在 中
中 ,
,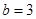 ,
, ,则
,则 =( )
=( )
A. | B.7 | C. | D.13 |
在△ABC中,其中有两解的是( )
| A.a=8,b=16,A=30° | B.a=30,b=25,A=150° |
| C.a=72,b=50,A=135° | D.a=18,b=20,A=60° |
 的内角
的内角 的对边分别为
的对边分别为 ,若
,若
 ,则边
,则边 等于( )
等于( )
A. | B. | C. | D.2 |
在 ABC中,
ABC中,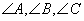 所对的边分别为a,b,c,已知a=2,b=
所对的边分别为a,b,c,已知a=2,b=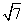 ,
,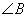 =
= ,则
,则 ABC的面积为
ABC的面积为
A.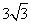 | B.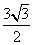 | C. | D. |
在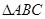 中,内角
中,内角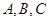 所对的边分别为
所对的边分别为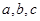 ,其中
,其中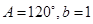 ,且
,且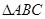 面积为
面积为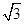 ,则
,则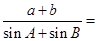 ( )
( )
A.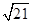 | B.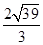 | C. | D.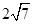 |
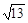
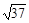
 、
、 、
、 ,若
,若 ,sinC=2
,sinC=2 sinB,则A=( )
sinB,则A=( )