题目内容
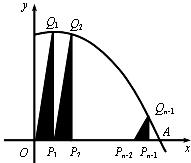
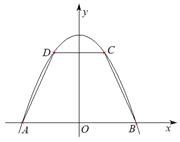
如图,抛物线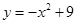 与
与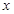 轴交于两点
轴交于两点 ,点
,点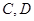 在抛物线上(点
在抛物线上(点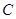 在第一象限),
在第一象限),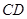 ∥
∥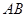 .记
.记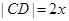 ,梯形
,梯形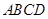 面积为
面积为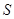 .
.
(Ⅰ)求面积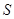 以
以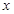 为自变量的函数式;
为自变量的函数式;
(Ⅱ)若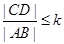 ,其中
,其中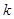 为常数,且
为常数,且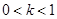 ,求
,求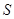 的最大值.
的最大值.
【答案】
(Ⅰ)解:依题意,点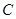 的横坐标为
的横坐标为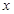 ,点
,点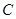 的纵坐标为
的纵坐标为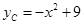 .
……1分
.
……1分
点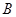 的横坐标
的横坐标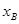 满足方程
满足方程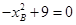 ,解得
,解得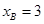 ,舍去
,舍去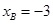 . ……2分
. ……2分
所以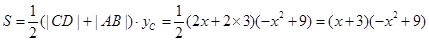 . ……4分
. ……4分
由点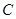 在第一象限,得
在第一象限,得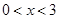 .
.
所以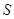 关于
关于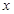 的函数式为
的函数式为 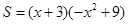 ,
,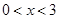 .…………5分
.…………5分
(Ⅱ)解:由 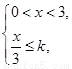 及
及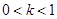 ,得
,得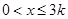 . ……………6分
. ……………6分
记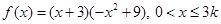 ,
,
则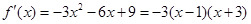 . ………………8分
. ………………8分
令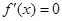 ,得
,得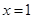 .
………………9分
.
………………9分
① 若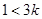 ,即
,即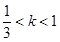 时,
时,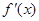 与
与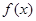 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
|
|
|
↗ |
极大值 |
↘ |
所以,当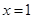 时,
时,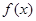 取得最大值,且最大值为
取得最大值,且最大值为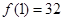 . …………11分
. …………11分
② 若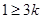 ,即
,即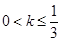 时,
时,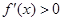 恒成立,[来源:学§科§网]
恒成立,[来源:学§科§网]
所以,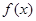 的最大值为
的最大值为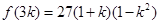 .
…………13分
.
…………13分
综上,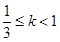 时,
时,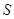 的最大值为
的最大值为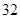 ;
;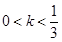 时,
时,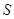 的最大值为
的最大值为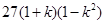 .
.
【解析】略

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
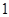
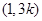
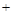
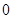
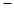
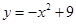 与
与 轴交于两点
轴交于两点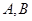 ,点
,点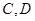 在抛物线上(点
在抛物线上(点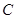 在第一象限),
在第一象限),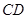 ∥
∥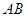 .记
.记 ,梯形
,梯形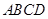 面积为
面积为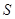 .
. 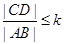 ,其中
,其中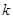 为常数,且
为常数,且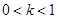 ,求
,求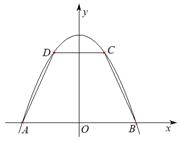
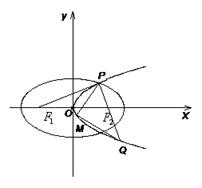
 的准线与
的准线与 轴交于
轴交于 ,焦点为
,焦点为 ;以
;以 为焦点,离心率
为焦点,离心率 的椭圆
的椭圆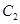 与抛物线
与抛物线 在
在 ,延长
,延长 交抛物线于点
交抛物线于点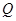 ,
, 是抛物线
是抛物线 时,求椭圆
时,求椭圆 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求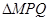 面积的最大值.
面积的最大值.