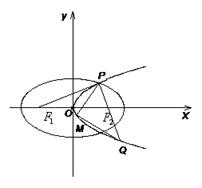
题目内容
如图,设抛物线![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,焦点为
,焦点为![]() ;以
;以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆
的椭圆![]() 与抛物线
与抛物线![]() 在
在![]() 轴上方的交点为
轴上方的交点为![]() ,延长
,延长![]() 交抛物线于点
交抛物线于点![]() ,
,![]() 是抛物线
是抛物线![]() 上一动点,且M在
上一动点,且M在![]() 与
与![]() 之间运动.
之间运动.
(1)当![]() 时,求椭圆
时,求椭圆![]() 的方程;
的方程;
(2)当![]() 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求![]() 面积的最大值.
面积的最大值.
(1)椭圆C2方程为![]()
(2)![]() 面积的最大值为
面积的最大值为![]() .
.
解析:
(1)当![]() 时,
时, ![]() ,则
,则![]()
设椭圆方程为![]() ,则
,则![]() 又
又![]() ,所以
,所以![]()
所以椭圆C2方程为![]() …………
…………![]() [来源:学§科§网Z§X§X§K]
[来源:学§科§网Z§X§X§K]
(2)因为![]() ,
,![]() ,则
,则![]() ,
,![]() ,设椭圆方程为
,设椭圆方程为![]()
由 ,得
,得![]() …………
…………![]() [来源:学科网ZXXK]
[来源:学科网ZXXK]
即![]() ,得
,得![]() 代入抛物线方程得
代入抛物线方程得![]() ,即
,即![]()
![]() ,
,![]() ,
,
因为![]() 的边长恰好是三个连续的自然数,所以
的边长恰好是三个连续的自然数,所以![]() …………
…………![]()
此时抛物线方程为![]() ,
,![]() ,直线
,直线![]() 方程为:
方程为:![]() .
.
联立 ,得
,得![]() ,即
,即![]() ,
,
所以![]() ,代入抛物线方程得
,代入抛物线方程得![]() ,即
,即![]()
∴![]() .
.
设![]() 到直线PQ的距离为
到直线PQ的距离为![]() ,
,![]()
则 …………
…………![]()
当![]() 时,
时,![]() ,
,
即![]() 面积的最大值为
面积的最大值为![]() . …………
. …………![]()

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
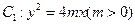 的准线与
的准线与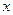 轴交于
轴交于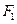 ,焦点为
,焦点为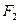 ;以
;以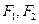 为焦点,离心率
为焦点,离心率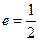 的椭圆
的椭圆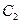 与抛物线
与抛物线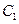 在
在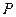 ,延长
,延长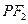 交抛物线于点
交抛物线于点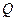 ,
,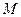 是抛物线
是抛物线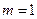 时,求椭圆
时,求椭圆 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求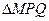 面积的最大值.
面积的最大值. 的准线与x轴交于点
的准线与x轴交于点 ,
, 为焦点,离心率为
为焦点,离心率为 的椭圆
的椭圆 与抛物线
与抛物线 在x轴上方的交点为P
在x轴上方的交点为P 交抛物线于点Q,M是抛物线
交抛物线于点Q,M是抛物线 且P点横坐标为
且P点横坐标为 ,求面积
,求面积 的最大值
的最大值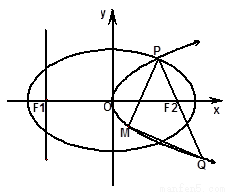
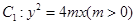 的准线与
的准线与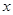 轴交于
轴交于 ,焦点为
,焦点为 ;以
;以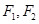 为焦点,离心率
为焦点,离心率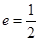 的椭圆
的椭圆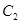 与抛物线
与抛物线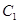 在
在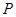 ,延长
,延长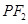 交抛物线于点
交抛物线于点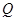 ,
,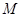 是抛物线
是抛物线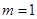 时,求椭圆
时,求椭圆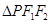 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时,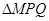 面积的最大值.
面积的最大值.
 的准线与
的准线与 轴交于
轴交于 ,焦点为
,焦点为 ;以
;以 为焦点,离心率
为焦点,离心率 的椭圆
的椭圆 与抛物线
与抛物线 在
在 ,延长
,延长 交抛物线于点
交抛物线于点 ,
, 是抛物线
是抛物线 时,求椭圆
时,求椭圆 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时, 面积的最大值.
面积的最大值.