题目内容
已知函数f(x)=x2+ax-lnx,a∈R
(1)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(2)令g(x)=f(x)-x2,是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由;
(3)求证:当x∈(0,e]时,e2x- >lnx+
>lnx+ .
.
(1)解:求导函数可得
因为函数f(x)在[1,2]上是减函数,所以 ≤0在[1,2]上恒成立,
≤0在[1,2]上恒成立,
令 h(x)=2x2+ax-1,有 得
得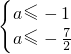 ,∴
,∴ ;
;
(2)解:假设存在实数a,使g(x)=ax-lnx(x∈(0,e])有最小值3,g′(x)=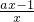
①当a≤0时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae-1=3,a=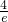 (舍去),
(舍去),
②当0< <e时,g(x)在(0,
<e时,g(x)在(0, )上单调递减,在(
)上单调递减,在( ,e]上单调递增
,e]上单调递增
∴g(x)min=g( ))=1+lna=3,a=e2,满足条件.
))=1+lna=3,a=e2,满足条件.
③当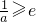 时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae-1=3,a=
时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae-1=3,a=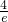 (舍去),
(舍去),
综上,存在实数a=e2,使g(x)=ax-lnx(x∈(0,e])有最小值3.
(3)证明:由(2)知当a=e2,g(x)=ax-lnx(x∈(0,e])有最小值3,即g(x)=e2x-lnx≥3
又原不等式成立只须e2x-lnx> +
+ 成立
成立
令F(x)= +
+ ,则F′(x)=
,则F′(x)=
当0<x≤e时,F'(x)≥0,∴F(x)在(0,e]上单调递增
故F(x)max=F(e)= 3
3
故当x∈(0,e]时,e2x- >lnx+
>lnx+ ,即原命题得证
,即原命题得证
分析:(1)求导函数,利用函数f(x)在[1,2]上是减函数,可得 ≤0在[1,2]上恒成立,考查函数h(x)=2x2+ax-1,即可确定a的取值范围;
≤0在[1,2]上恒成立,考查函数h(x)=2x2+ax-1,即可确定a的取值范围;
(2)求导函数,分类讨论,确定函数的单调性,利用函数g(x)的最小值是3,即可求出a的值;
(3)原不等式成立只须e2x-lnx> +
+ 成立.利用g(x)=e2x-lnx≥3,证明
成立.利用g(x)=e2x-lnx≥3,证明 +
+ <3即可.
<3即可.
点评:本题主要考查导数的运算和函数的单调性与其导函数的正负之间的关系,当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

因为函数f(x)在[1,2]上是减函数,所以
 ≤0在[1,2]上恒成立,
≤0在[1,2]上恒成立,令 h(x)=2x2+ax-1,有
 得
得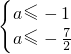 ,∴
,∴ ;
;(2)解:假设存在实数a,使g(x)=ax-lnx(x∈(0,e])有最小值3,g′(x)=
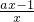
①当a≤0时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae-1=3,a=
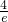 (舍去),
(舍去),②当0<
 <e时,g(x)在(0,
<e时,g(x)在(0, )上单调递减,在(
)上单调递减,在( ,e]上单调递增
,e]上单调递增∴g(x)min=g(
 ))=1+lna=3,a=e2,满足条件.
))=1+lna=3,a=e2,满足条件.③当
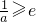 时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae-1=3,a=
时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae-1=3,a=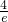 (舍去),
(舍去),综上,存在实数a=e2,使g(x)=ax-lnx(x∈(0,e])有最小值3.
(3)证明:由(2)知当a=e2,g(x)=ax-lnx(x∈(0,e])有最小值3,即g(x)=e2x-lnx≥3
又原不等式成立只须e2x-lnx>
 +
+ 成立
成立令F(x)=
 +
+ ,则F′(x)=
,则F′(x)=
当0<x≤e时,F'(x)≥0,∴F(x)在(0,e]上单调递增
故F(x)max=F(e)=
 3
3故当x∈(0,e]时,e2x-
 >lnx+
>lnx+ ,即原命题得证
,即原命题得证分析:(1)求导函数,利用函数f(x)在[1,2]上是减函数,可得
 ≤0在[1,2]上恒成立,考查函数h(x)=2x2+ax-1,即可确定a的取值范围;
≤0在[1,2]上恒成立,考查函数h(x)=2x2+ax-1,即可确定a的取值范围;(2)求导函数,分类讨论,确定函数的单调性,利用函数g(x)的最小值是3,即可求出a的值;
(3)原不等式成立只须e2x-lnx>
 +
+ 成立.利用g(x)=e2x-lnx≥3,证明
成立.利用g(x)=e2x-lnx≥3,证明 +
+ <3即可.
<3即可.点评:本题主要考查导数的运算和函数的单调性与其导函数的正负之间的关系,当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|