题目内容
已知平面凸四边形ABCD的边长均大于2,且∠DAB=45°,点P在四边形ABCD内运动,且在AB、AD上的射影分别为M、N,若PA=2,则△PMN面积的最大值为 .
考点:两角和与差的正弦函数,正弦定理
专题:三角函数的求值
分析:设∠PAM=α,求出PM、PN,然后利用两角和与差的三角函数化简表达式,通过三角函数的最值求解即可.
解答:
 解:如图设∠PAM=α,PM=2sinα,PN=2sin(45°-α),
解:如图设∠PAM=α,PM=2sinα,PN=2sin(45°-α),
△PMN面积S=
PM•PNsin135°=
sinαsin(45°-α)
=sinαcosα-sin2α
=
sin2α-
(1-cos2α)
=
sin(2α+45°)-
.
∵α∈[0°,45°],2α+45°∈[45°,135°],
sin(2α+45°)-
≤
-
.
三角形面积的最大值为:
-
.
故答案为:
-
.
 解:如图设∠PAM=α,PM=2sinα,PN=2sin(45°-α),
解:如图设∠PAM=α,PM=2sinα,PN=2sin(45°-α),△PMN面积S=
| 1 |
| 2 |
| 2 |
=sinαcosα-sin2α
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
∵α∈[0°,45°],2α+45°∈[45°,135°],
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
三角形面积的最大值为:
| ||
| 2 |
| 1 |
| 2 |
故答案为:
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查两角和与差的三角函数,三角函数的最值的求法,考查计算能力.

练习册系列答案
相关题目
| ∫ | 2 1 |
| 1 |
| x |
| A、1 | B、2 | C、ln2 | D、-ln2 |
 如图,BC为圆O的直径,D为圆周上异于B、C的一点,AB垂直于圆O所在的平面,BE⊥AC于点E,BF⊥AD于点F.
如图,BC为圆O的直径,D为圆周上异于B、C的一点,AB垂直于圆O所在的平面,BE⊥AC于点E,BF⊥AD于点F.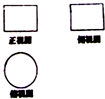 如图所示的是一个立体图形的三视图,此立体图形的名称为:
如图所示的是一个立体图形的三视图,此立体图形的名称为: