题目内容
已知圆M：（x-2）2+（y-3）2=1与圆N：x2+y2+2x+2ay+a2-15=0外切，则a= ．
【答案】分析：求出两个圆的圆心坐标和半径，利用两个圆的圆心距等于半径和，即可求出a的取值范围．
解答：解：圆M：（x-2）2+（y-3）2=1，
其圆心为（2，3），半径r=1，
圆N：x2+y2+2x+2ay+a2-15=0，化为：（x+1）2+（y+a）2=16其圆心为（-1，-a），半径为r=4，
根据两圆相切的充要条件：两个圆的圆心距等于半径和，得
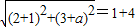
解得a=1
故答案为：1．
点评：本题考查了圆的标准方程的化简及两个圆的位置关系，注意两个圆的位置关系的各种形式，圆心距与半径和与差的大小比较，考查计算能力，转化思想．
解答：解：圆M：（x-2）2+（y-3）2=1，
其圆心为（2，3），半径r=1，
圆N：x2+y2+2x+2ay+a2-15=0，化为：（x+1）2+（y+a）2=16其圆心为（-1，-a），半径为r=4，
根据两圆相切的充要条件：两个圆的圆心距等于半径和，得
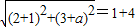
解得a=1
故答案为：1．
点评：本题考查了圆的标准方程的化简及两个圆的位置关系，注意两个圆的位置关系的各种形式，圆心距与半径和与差的大小比较，考查计算能力，转化思想．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目