题目内容
已知O是四边形ABCD所在平面内任一点,且|
+
|=|(
)+(
)|,
∥
,则四边形ABCD的形状是
| AO |
| OB |
| DO |
| OC |
| AB |
| CD |
平行四边形
平行四边形
.分析:利用向量的运算法则化简已知等式,利用向量共线则表示向量的有向线段平行;利用平行四边形的定义得到答案.
解答:解:由条件知|
|=|
|,又
∥
,
∴AB∥CD,AB=CD
∴四边形为平行四边形.
故答案为:平行四边形
| AB |
| DC |
| AB |
| CD |
∴AB∥CD,AB=CD
∴四边形为平行四边形.
故答案为:平行四边形
点评:本题考查向量的运算法则、考查平行四边形的定义、考查向量共线的定义.

练习册系列答案
相关题目
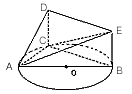
 如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行 (1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
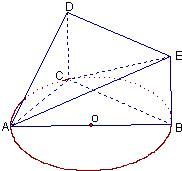
(1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB. 如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,又DC⊥面ABC,四边形ACDE为梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小为θ,tan
如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,又DC⊥面ABC,四边形ACDE为梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小为θ,tan 平面ABC ,
平面ABC , ,已知AE与平面ABC所成的角为
,已知AE与平面ABC所成的角为 ,且
,且 .
. ;
; ,
, 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求
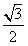 。
。