题目内容
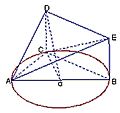
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,已知AE与平面ABC所成的角为θ,且tanθ=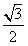 。
。
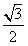 。
。 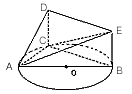
(Ⅰ)证明:平面ACD⊥平面ADE;
(Ⅱ)记AC=x,V(x)表示三棱锥A-CBE的体积,求V(x)的表达式;
(Ⅲ)当V(x)取得最大值时,求二面角D-AB-C的大小。
(Ⅱ)记AC=x,V(x)表示三棱锥A-CBE的体积,求V(x)的表达式;
(Ⅲ)当V(x)取得最大值时,求二面角D-AB-C的大小。
| (Ⅰ)证明:∵四边形DCBE为平行四边形, ∴CD∥BE,BC∥DE, ∵DC⊥平面ABC,BC  平面ABC, 平面ABC,∴DC⊥BC, ∵AB是圆O的直径, ∴BC⊥AC且DC∩AC=C, ∴BC⊥平面ADC, ∵DE∥BC,∴DE⊥平面ADC, 又∵DE  平面ADE, 平面ADE,∴平面ACD⊥平面ADE。 (Ⅱ)解:∵DC⊥平面ABC, ∴BE⊥平面ABC, ∴∠EAB为AE与平面ABC所成的角,即∠EAB =θ, 在Rt△ABE中,由 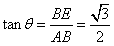 ,AB=2得 ,AB=2得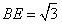 , ,在Rt△ABC中, ∵ 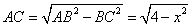 (0<x<2), (0<x<2),∴ 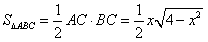 , ,∴  (0<x<2)。 (0<x<2)。 |
|
|
(Ⅲ)解:由(Ⅱ)知0<x<2, |
 |

练习册系列答案
相关题目
 要取得最大值,
要取得最大值, 取得最大值,
取得最大值, 当且仅当
当且仅当 ,
, 时,“=”成立,
时,“=”成立, 取得最大值时,
取得最大值时, ,这时△ACB为等腰直角三角形,
,这时△ACB为等腰直角三角形, ≌
≌ ,
, ,
, ,
, ,
, 取得最大值时,二面角D-AB-C为60°。
取得最大值时,二面角D-AB-C为60°。 如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=
如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=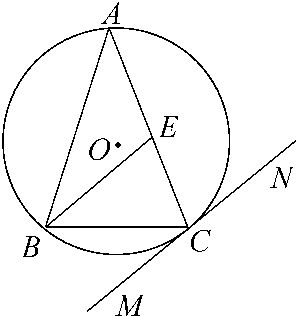 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.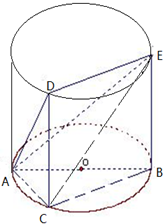 如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=
如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=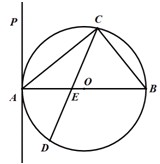 (2013•沈阳二模)选修4-1:几何证明选讲
(2013•沈阳二模)选修4-1:几何证明选讲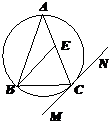 如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )
如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )