题目内容
如图2-25,经过点A、C的圆O切AB于点A,交CB于点D,∠ABC的平分线BG交⊙O于点G,作∠GAE =∠GAB,AE交CG于F点,交CD于E点,求证: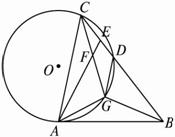
图2-25
(1)∠EDG =∠EFG;
(2)AG2 =CG·DG.
思路分析:(1)要证∠EDG =∠EFG,只需证∠GDB =∠AFG,而∠GDB =∠CAG,∠AFG =∠GCA +∠CAF,由∠GAB为弦切角,用弦切角定理证明即可;?
(2)由(1)易证△AFG∽△CAG,从而得AG2=CF·CG,故再证FG =DG,连结EG,证△EFG≌△EDG就能达到目的.
证明:(1)∵四边形AGDC是圆内接四边形,?
∴∠EDG +∠CAG =180°.?
∵∠EFG =∠AFC,?
∴∠EFG +∠ACF +∠CAF =180°.?
∵∠ACF =∠BAG,∠BAG =∠FAG,?
∴∠EFG +∠BAG+∠CAF =∠EFG+∠FAG +∠CAF =180°.?
∴∠EFG +∠CAG =180°.∴∠EDG =∠EFG.?
(2)连结EG,?
∵∠AFG =∠ACF +∠CAF,∠ACF =∠BAG =∠FAG,?
∴∠AFG =∠CAG.?
又∵∠AGC公用,∴△AGF∽△CGA.?
∴![]() =
=![]() .?
.?
∵GA平分∠EAB,BG平分∠ABD,?
∴G到AE、B、BE的距离相等(即G为△ABE的内心).?
∴G在∠AEB的角平分线上.?
∴∠FEG =∠DEG.?
∵EG =EG,∠EDG =∠EFG,∴△FEG≌△DEG.?
∴FG =DG.?
∴![]() =
=![]() ,即AG2=CG·DG.
,即AG2=CG·DG.

练习册系列答案
相关题目
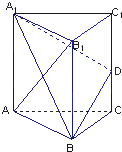 如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱C C1到点A1的最短路线长为2
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱C C1到点A1的最短路线长为2 如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反向后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反向后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( ) 如图为一个观览车示意图,该观览车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离为h.
如图为一个观览车示意图,该观览车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离为h.