题目内容
已知P(x,y)为函数y=lnx图象上一点,O为坐标原点.记直线OP的斜率k=f(x).(I)同学甲发现:点P从左向右运动时,f(x)不断增大,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的判断.
(Ⅱ)求证:当x>1时,f(x)<
| x-1 | ||
x
|
(III)同学乙发现:总存在正实数a、b(a<b),使ab=ba.试问:他的判断是否正确?若不正确,请说明理由:若正确,请求出a的取值范围.
分析:(I)同学甲的判断不正确.f′(x)=
,当x∈(0,e)时,f′(x)>0;当x∈(e,+∞)时,f′(x)<0,故f(x)在(0,e]上递增,在[e,+∞)递减.
(Ⅱ)f(x)-
=
-
=
,记g(x)=lnx-
+
,g′(x)=
-
x
-
x-
=-
x
(
-1)2<0,g(x)在(1,+∞)为减函数,由此能够证明f(x)<
.
(III)同学乙的判断正确.
=0,且
>0(x>1),f(x)<
,当x→∞时,f(x)→0,由此能求出求出a的取值范围.
| 1-lnx |
| x2 |
(Ⅱ)f(x)-
| x-1 | ||
x
|
| lnx |
| x |
| x-1 | ||
x
|
lnx-
| ||||||
| x |
| x |
| 1 | ||
|
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| x |
| x-1 | ||
x
|
(III)同学乙的判断正确.
| lim |
| x→+∞ |
| x-1 | ||
x
|
| x-1 | ||
x
|
| x-1 | ||
x
|
解答:解:(I)同学甲的判断不正确.
依题意,f(x)=
,f′(x)=
,
当x∈(0,e)时,f′(x)>0;当x∈(e,+∞)时,f′(x)<0,
∴f(x)在(0,e]上递增,在[e,+∞)递减.
(Ⅱ)f(x)-
=
-
=
,
记g(x)=lnx-
+
,
g′(x)=
-
x
-
x-
=-
x
(
-1)2<0,
∴g(x)在(1,+∞)为减函数,
则g(x)=lnx-
+
<g(1)=0,
∴f(x)-
<0,即f(x)<
.
(III)同学乙的判断正确.
∵
=0,且
>0(x>1),
又由(2)f(x)<
,
∴当x→∞时,f(x)→0,
∴总存在正实数a,b,且1<a<e<b,使得f(a)=f(b),即
=
,∴ab=ba,此时1<a<e.
依题意,f(x)=
| lnx |
| x |
| 1-lnx |
| x2 |
当x∈(0,e)时,f′(x)>0;当x∈(e,+∞)时,f′(x)<0,
∴f(x)在(0,e]上递增,在[e,+∞)递减.
(Ⅱ)f(x)-
| x-1 | ||
x
|
| lnx |
| x |
| x-1 | ||
x
|
lnx-
| ||||||
| x |
记g(x)=lnx-
| x |
| 1 | ||
|
g′(x)=
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| x |
∴g(x)在(1,+∞)为减函数,
则g(x)=lnx-
| x |
| 1 | ||
|
∴f(x)-
| x-1 | ||
x
|
| x-1 | ||
x
|
(III)同学乙的判断正确.
∵
| lim |
| x→+∞ |
| x-1 | ||
x
|
| x-1 | ||
x
|
又由(2)f(x)<
| x-1 | ||
x
|
∴当x→∞时,f(x)→0,
∴总存在正实数a,b,且1<a<e<b,使得f(a)=f(b),即
| lna |
| a |
| lnb |
| b |
点评:本题考查导数在函数的单调性中的应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地借导数性质进行解答.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 已知y=Asin(ωx+?)的最大值为1,在区间[
已知y=Asin(ωx+?)的最大值为1,在区间[| π |
| 6 |
| 2π |
| 3 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、以上都不是 |
 上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )
上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )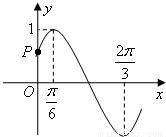



 -2lnx、
-2lnx、