题目内容
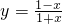的单调递减区间是________．
（-∞，-1）和（-1，+∞）
分析：利用分离常数法对函数解析式化简，根据y=
=-1+
的图象可由y=
向左平移1个单位，再向下平移1个单位
画出函数的图象，可得单调区间．
解答：
解：∵y==-1+，
∴定义域为（-∞，-1）∪（-1，+∞），
y==-1+可由y=向左平移1个单位，再向下平移1个单位
画出函数的图象，如右图
结合图象可知该函数的递减区间为（-∞，-1）和（-1，+∞）．
故答案为：（-∞，-1）和（-1，+∞）．
点评：本题考查了判断函数的单调性和求单调区间，以及函数的图象与性质，属于基础题．
分析：利用分离常数法对函数解析式化简，根据y=
=-1+的图象可由y=向左平移1个单位，再向下平移1个单位画出函数的图象，可得单调区间．
解答：
解：∵y==-1+，∴定义域为（-∞，-1）∪（-1，+∞），
y=
=-1+可由y=向左平移1个单位，再向下平移1个单位画出函数的图象，如右图
结合图象可知该函数的递减区间为（-∞，-1）和（-1，+∞）．
故答案为：（-∞，-1）和（-1，+∞）．
点评：本题考查了判断函数的单调性和求单调区间，以及函数的图象与性质，属于基础题．
练习册系列答案
相关题目
函数y=f（x）的导函数y=f′（x）的图象是如图所示的一条直线，则y=f（x）的单调递减区间是（ ）| A、（-∞，+∞） | B、（-∞，1） | C、（1，+∞） | D、（0，1） |