题目内容
正方体A1B1C1D1-ABCD的棱长为1，则下列四个问题
（1）对角线A1C与所有棱所成角的正切值都等于
（2）点A、C到面BC1D的距离相等
（3）AD1与面BC1D所成角为0°
（4）面A1ACC1⊥面BC1D
其中正确的个数有（ ）
（1）对角线A1C与所有棱所成角的正切值都等于
| 2 |
（2）点A、C到面BC1D的距离相等
（3）AD1与面BC1D所成角为0°
（4）面A1ACC1⊥面BC1D
其中正确的个数有（ ）
分析：利用空间角的定义和距离公式和面面垂直的判定定理分别判断．
解答：
解：（1）根据正方体的对称性可知对角线A1C与所有棱所成角都相同，则对应的角的正切值为tanA1CB=
=
，
所以（1）正确．
（2）如图，连结AP，则AP∥面BC1D，所以点A到平面BC1D的距离和点P到平面BC1D的距离相等，又因为OCC1P为矩形，所以C，P到平面BC1D的距离相等，
所以点A、C到面BC1D的距离相等，所以（2）正确．
（3）因为AD1?ABC1D1，所以AD1?面BC1D，所以AD1与面BC1D所成角为0°，
所以（3）正确．
（4）在正方体中，BD⊥AA1C1C，因为BD?BC1D，所以面A1ACC1⊥面BC1D成立，
所以（4）正确．
故正确的个数有4个．
故选D．
解：（1）根据正方体的对称性可知对角线A1C与所有棱所成角都相同，则对应的角的正切值为tanA1CB=| A1B |
| BC |
| 2 |
所以（1）正确．
（2）如图，连结AP，则AP∥面BC1D，所以点A到平面BC1D的距离和点P到平面BC1D的距离相等，又因为OCC1P为矩形，所以C，P到平面BC1D的距离相等，
所以点A、C到面BC1D的距离相等，所以（2）正确．
（3）因为AD1?ABC1D1，所以AD1?面BC1D，所以AD1与面BC1D所成角为0°，
所以（3）正确．
（4）在正方体中，BD⊥AA1C1C，因为BD?BC1D，所以面A1ACC1⊥面BC1D成立，
所以（4）正确．
故正确的个数有4个．
故选D．
点评：本题主要考查空间直线，平面之间距离和夹角的求法，要求熟练掌握空间角和空间距离的定义和公式．
练习册系列答案
相关题目
7、如图，正方体ABCD-A1B1C1D中，P为平面A1ABB1内一动点，且点P到A1A和BC的距离相等，则P点的轨迹是下图中的（ ）
如图，在正方体ABCD-A1B1C1D中，异面直线A1D与D1C所成的角为
如图：正方体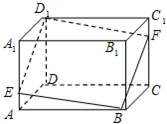
已知E，F分别是正方体ABCD-A1B1C1D的棱AA1和棱CC1上的点，且AE=C1F，求证：四边形EBFD1是平行四边形．