题目内容
已知函数f（x）的反函数是
，那么f（4-x2）的单调减区间是________．
（-2，0]
分析：先求出的反函数f（x），得出f（4-x2）的表达式，先确定此函数的定义域，再找出的4-x2大于0时的单调增区间，进而得到 f（4-x2）的单调减区间．
解答：∵f（x）的反函数为，
∴f（x）=
，
f（4-x2）=
，
一方面，4-x2＞0，另一方面，考察函数t=4-x2的单调增区间，
∴在（-2，0]上函数值y=f（4-x2）随自变量x的增大而减小，
故答案为：（-2，0]．
点评：本题考查求反函数的方法、考查函数单调性的应用、等式的解法等基础知识，考查运算求解能力与转化思想．属于基础题．
分析：先求出
的反函数f（x），得出f（4-x2）的表达式，先确定此函数的定义域，再找出的4-x2大于0时的单调增区间，进而得到 f（4-x2）的单调减区间．解答：∵f（x）的反函数为
，∴f（x）=
，f（4-x2）=
，一方面，4-x2＞0，另一方面，考察函数t=4-x2的单调增区间，
∴在（-2，0]上函数值y=f（4-x2）随自变量x的增大而减小，
故答案为：（-2，0]．
点评：本题考查求反函数的方法、考查函数单调性的应用、等式的解法等基础知识，考查运算求解能力与转化思想．属于基础题．
练习册系列答案
相关题目
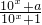是奇函数．
的反函数为f-1(x)=
(x≥0),则由函数f(x)=2
确定的数列{an}的反数列为{bn},求{bn}的通项公式;不等式
+
+…+
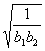≥1-2a对任意的正整数n恒成立,求实数a的范围;