题目内容
17.已知奇函数f(x)在区间(-∞,0)上是增函数,且f(-2)=-1,f(1)=0,当x1>0,x2>0有f(x1x2)=f(x1)+f(x2),求不等式log2|f(x)+1|<0的解集.分析 根据对数函数的单调性将不等式进行转化,根据函数奇偶性和单调性的关系以及抽象函数关系,利用特殊值法进行求解即可.
解答 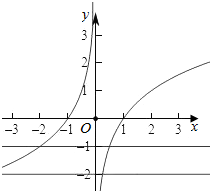 解:不等式log2|f(x)+1|<0等价为0<|f(x)+1|<1,
解:不等式log2|f(x)+1|<0等价为0<|f(x)+1|<1,
即0<f(x)+1<1或-1<f(x)+1<0,
即-1<f(x)<0或-2<f(x)<-1,
∵f(x)是奇函数,且且f(-2)=-1,f(1)=0,
∴f(2)=1,
∵当x1>0,x2>0有f(x1x2)=f(x1)+f(x2),
∴函数f(x)为对数函数模型,
即当x>0时,设f(x)=logax,
∵奇函数f(x)在区间(-∞,0)上是增函数,
∴函数f(x)在区间(0,+∞)上是增函数,
则a>1,
∵f(2)=1,∴f(2)=loga2=1,则a=2,
即当x>0时,f(x)=log2x,
若x<0,则-x>0,则f(-x)=log2(-x)=-f(x),
即f(x)=-log2(-x),x<0,
则函数f(x)的图象如图:
若x>0,由-1<f(x)<0或-2<f(x)<-1得-1<log2x<0或-2<log2x<-1,
即$\frac{1}{2}$<x<1或$\frac{1}{4}$<log2x<$\frac{1}{2}$,
若x<0,由-1<f(x)<0或-2<f(x)<-1得-1<-log2(-x)<0或-2<-log2(-x)<-1,
即0<log2(-x)<1或1<log2(-x)<2,
即1<-x<2或2<-x<4,
即-2<x<-1或-4<x<-2,
综上不等式的解集为(-4,-2)∪(-2,-1)∪($\frac{1}{2}$,1)∪($\frac{1}{4}$,$\frac{1}{2}$).
点评 本题主要考查不等式的求解,根据抽象函数关系转化为对数函数模型是解决本题的关键.根据函数奇偶性和单调性的关系结合数形结合进行求解是解决本题的突破点.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{3}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |