题目内容
正方体ABCD—A1B1C1D1中,E、F分别是AB、B1C的中点,则EF与平面ABCD所成的角的正切值为( ) 
A. 2
B. 
C. 
D. 
D
解析试题分析:设正方体的棱长为a,取BC得中点M,连接ME,MF,由正方体的性质可知MF⊥平面ABCD,则∠MEF即为直线EF与平面ABCD所成的角。在Rt△MEF中,∠FME=90°,FM= a,ME=
a,ME= a,所以tan∠FEM=
a,所以tan∠FEM= 。故选D。
。故选D。
考点:直线与平面所成的角。
点评:本题主要考查了直线与平面所成的角的求解,解题的关键是熟练利用正方体的性质要找到已知平面ABCD的垂线,然后在直角三角形中求解。

练习册系列答案
相关题目
椭圆 的长轴为
的长轴为
 ,短轴为
,短轴为
 ,将椭圆沿y轴折成一个二面角,使得
,将椭圆沿y轴折成一个二面角,使得 点在平面
点在平面

 上的射影恰好为椭圆的右焦点,则该二面角的大小为( ).
上的射影恰好为椭圆的右焦点,则该二面角的大小为( ).
| A.75° | B.60° | C.45° | D.30° |
如图长方体中,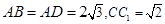 ,则二面角
,则二面角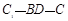 的大小为
的大小为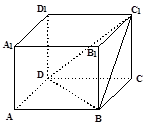
| A.300 | B.450 | C.600 | D.900 |
在棱长为a的正方体 中,M是AB的中点,则点C到平面
中,M是AB的中点,则点C到平面 的距离为( )
的距离为( )
A. | B. | C. | D. |
已知正三棱柱ABC—A1B1C1中,A1B⊥CB1,则A1B与AC1所成的角为( )
| A.450 | B.600 | C.900 | D.1200 |
若 ,且
,且 ,OA与O1A1的方向相同,则下列结论正确的是( )
,OA与O1A1的方向相同,则下列结论正确的是( )
A. 且方向相同 且方向相同 | B. |
| C.OB与O1B1不平行 | D.OB与O1B1不一定平行 |
已知 是两条不同直线,
是两条不同直线, 是三个不同平面,下列命题正确的是( )
是三个不同平面,下列命题正确的是( )
A. |
B. |
C. |
D. |
垂直于同一条直线的两条直线一定( )
| A.平行 | B.相交 | C.异面 | D.以上都有可能 |



